Gravity 03: Curvature & the Landscape of the Cosmos

by Shane L. Larson

Had he been alive when Queen formed in 1970, perhaps Einstein might have jammed with them.

“Is this the real life? Is this just fantasy?”  So opens the classic rock song by Queen, Bohemian Rhapsody. Trying to understand modern gravity often puts one in the frame of mind that the mental machinations we go through are somehow not connected to reality. Albert Einstein’s genius was that he persevered through those uncomfortable feelings. He willfully ignored traditional ways of thinking about the real world, and imagined new and inventive ways to describe how Nature behaves.

One of those inventive ways of thinking was to noodle about unusual situations, like the Equivalence Principle. What a happy little thought — an idle daydream to imagine an elevator on the Earth, or flying in a rocket, and asking what would happen if you did something as simple as drop an apple? Dropping an apple is an act of everyday life, but the conclusion seemed almost a fantasy. Einstein’s thought experiment had discerned that there was no way for a person to distinguish if they are in a rocket controlled elevator, or under the influence of the gravity from a planet. At face value, the conclusions would seem to be this: since I can’t tell the difference between gravity and a rocket, maybe gravity isn’t real at all.

Any normal person might throw up their hands in exasperation and decide this discussion of the Equivalence Principle is nonsense and go work on something simpler (like brain neurochemistry). But Einstein was a persistent fellow, and pushed a little harder.  He asked, “Is this the real life? Is this just fantasy?” Could it really be the case that there is no way to tell if you are in a gravitational field? What can we experience — what can we observe — that convinces us that we are caught in the grip of gravity?

We understand the world through experiments; they are the medium by which we observe. All experiments — thought experiments in particular — are recipes. Experiments produce results (knowledge about the Cosmos) the same way a recipe produces a cookie. We look at that result, and we ask ourselves a few fundamental questions — they are the same for physics experiments as cookies. Why is the result this way? Can I change what went into the result? Will I get a different result if I change what I put in?

Science and baking are both built around experiments that seek to discover what small changes reveal about the world. In cookies, a relatively small change can change a chocolate cookie into an almost identical vanilla cookie (TOP). A more substantial but not completely different approach might make a peanut butter cookie (BOTTOM). But getting a chocolate chip cookie (RIGHT) takes a completely different approach. [Photo by S. Larson; I don’t know what happened to these cookies after the #science was done; sorry.]

Science is a game of tearing apart ideas and seeing what makes them tick. Changing the assumptions, the recipe of the experiment, could change the outcome. So once again, Einstein returned to our thought experiment with the elevators, and imagined something new. There is a big assumption hidden in our thought experiment — the rooms you and I were confined to were “small.”

Why should that matter? Let’s imagine that our rooms were larger — much larger — and consider each of them in turn.

First, think about your room, on a spaceship. This is a BIG spaceship, of the sort that only the Galactic Empire has the metal and economic resources to build. The entire bottom of the spaceship is covered by rockets, all of them pushing with the same force to make you go.  Now conduct the apple dropping experiment again, first at one end of the spaceship, and then at the other end, very far away.  Both apple drops show the same thing — the apple falls directly down, parallel to the walls of your spaceship.

No matter how large you make a room, if it is being propelled uniformly by rockets, apples all over the room fall straight to the floor, along paths that are everywhere parallel to one another.

Now think about my room, on the planet Earth. This is a BIG room, far larger than any room ever built as it is large enough that if my floors are flat, the curvature of the Earth falls away from under my room at both ends (though I am not aware of this — no windows, right?). If I drop my apple at either end of my huge room I make an astonishing discovery — my apple does not fall parallel to the wall! It lands farther from the wall than it started. Given the outcome of my experiment, I could imagine all sorts of plausible explanations.

Perhaps the walls of my gigantic room are repulsive.

Maybe the walls are repulsive!

That’s an interesting idea; maybe it’s true, maybe it’s not. Can I test it?

Sure!  I build a few new walls at different places in the big room and drop many apples many times. What I find is this: if a wall is closer to the center of the room, a dropped apple falls closer to straight down. At the exact center of the room, two apples fall straight down and land the same distance apart as when they were released. Two apples dropped at opposite ends of the room are closer together when they land on the floor! Physicists get grandiloquent about this and call it “tidal deviation.”

What is going on? The walls clearly aren’t repulsive — a wall in the center of the room doesn’t push apples away from it at all.  We have talked about the lines of force that show the gravitational field.  The gravitational field always points to the center of the source of gravity. What this experiment seems to show is that if my room is big enough, I can detect the shape of the gravitational field!

(TOP) When my apples are dropped, their paths are not parallel; we say there is a tidal deviation between the paths. This is a key experimental signature of gravity. (BOTTOM) We can understand the tidal deviation of the apple paths if we imagine they are following the lines of force in the gravitational field (this is how Newton would have explained it). But this is not the only way to explain gravity!

This idea of the shape of the gravitational field, and its relation to the motion of falling objects, would be a key part of Einstein’s mathematical development of general relativity: it led him to the thought that motion and geometry could be connected.

That may seem like an odd thought, but the fundamental building blocks of elementary geometry are exactly the elements of motion that we discovered in our Giant Room Apple Dropping Experiments: lines can be parallel or not parallel. Einstein recognized that was important, so he explored it. We can too! Let’s think about a flat table top.

If I have two Matchbox cars on my table, and give them a push, they travel in a straight line and never stop (in the absence of friction — every little kid’s dream!).  If I take those two cars and set them in motion  exactly parallel to one another, what happens? The two cars speed off across the table and their paths never cross, no matter how far they go. In many ways, this example is like our two apples on opposite ends of the Gigantic Rocket-Propelled Room — the apples both started falling on straight lines, parallel to each other, and they ended up hitting the floor falling on straight lines that were still parallel to each other.

On a flat surface, two lines that begin parallel stay parallel, no matter how far you extend the lines across the surface.

So this leads to the inevitable question: is there a way in geometry to make the Matchbox cars start out along parallel paths, but ultimately draw closer together? This would be analogous to the Gigantic Room the size of Earth, where apples dropped on opposite ends of the room landed closer together.  As it turns out, the answer to this question is YES.

Imagine a sphere, like a playground ball or a desk globe.  The surface of the globe is two dimensional, just like the table top — there are only two directions you can go: front-back, or left-right. Suppose I take my two cars and set them on the equator in different spots, but both are initially travelling due north — the paths are parallel! What happens? Eventually, the paths of the two cars get closer together, and if we wait long enough, they cross.

If two travellers start at the equator travelling due north, their paths are initially parallel. By the time they reach the top of the globe, their paths cross each other — the paths don’t remain parallel because of the curvature of the globe!

Now, that is no way for parallel lines to behave on a piece of flat two-dimensional paper, but it is perfectly acceptable on a two-dimensional curved surface. THIS is the watershed idea of general relativity — maybe we can describe gravity as curvature. Maybe we can replace the concept of a gravitational force with the idea of particles moving on a curved surface — on flat surfaces, motion along parallel paths stay parallel, but on curved surfaces initially parallel pathways can converge and cross.

Neat idea. But curvature of what?!

Different ways we have devised to measure space or time.

Einstein brilliantly deduced that since our concern is with the motion of things, it should be curvature of the quantities that we use to describe motion — space and time. Special relativity, which motivated our reconsideration of gravity, was wholly focused on how we measure space and time, and Einstein’s former professor, Hermann Minkowski, had discovered that individually space and time are artificial elements of a single medium — spacetime.  Spacetime is the fabric of the Cosmos, the medium on which all things move. Einstein had become well versed in this notion, and concluded:

Gravity is the curvature of spacetime.

This is the heart of general relativity. So how does it work? General relativity is summarized mathematically by 10 coupled, non-linear, partial differential equations known as the Einstein Field Equations, succinctly written as

Fortunately for us, this mathematics can be captured in a simple, two-line mantra to guide intuition:

Space tells matter how to move.

Matter tells space how to curve.

In geometric gravity — general relativity — you can imagine spacetime like a large, deformable sheet. A particle can move anywhere on that sheet, so long as it stays on the sheet.  In places where the sheet is flat (“flat space”) the particle moves in an absolutely straight line.

But what happens if a particle encounters a large depression on the sheet? The only rule is the particle has to stay in contact with the sheet. It continues to travel in the straightest line it can, but if its path dips down into the depression, the direction the particle is travelling is slightly altered, such that when it emerges on the far side, it is travelling in a new direction that is not parallel to its original course!  Space tells matter how to move, with its shape.

Far from sources of gravity (edges of the sheet) spacetime is flat, and objects travel on straight lines. Small masses warp spacetime into a gravitational well (left dimple), while larger masses make larger gravitational wells (right dimple). If a particle comes close to a gravitational well, the curvature of spacetime bends its pathway. If a particle gets trapped in a gravitational well, the curvature of spacetime forces it to travel on a closed pathway — an orbit.

How do you curve spacetime?  With matter. The large, deformable sheet of spacetime is dimpled wherever there is a large concentration of mass; the larger the mass, the larger the dimple. Matter tells space how to curve, with its mass.  The larger the dimple, the larger deflection a particle passing nearby will feel. This at last, is the long awaited connection to the way we think about Newtonian gravity — the source of gravity is always matter, as we expected.

So we have done away with the concept of a “gravitational force field” and replaced it with the idea of “motion on a curved spacetime.” An astute reader will ask a pertinent question: if general relativity is really the way gravity works, why didn’t we discover it first? Where did Newtonian gravity come from?

Both Newtonian gravity and general relativity make exactly the same predictions when gravity is weak and speeds are slow.  In fact, mathematically, general relativity looks just like Newtonian gravity at slow speeds and in weak gravity. These are precisely the conditions we encounter in the solar system, which is why Newtonian gravity was discovered first, instead of general relativity!

You may have encountered models of spacetime gravitational wells out in the world. This one, in the Milwaukee Airport, captures coins for a museum. [Photo by K. Breivik]

It’s fine, of course, to make up a new idea about gravity. But this is science — fancy theories are only as good as the tests that can be conducted to verify them.  Einstein knew this, and proposed a series of tests for general relativity, which we’ll talk about next time.

PS: I rather enjoyed using Bohemian Rhapsody to start this bit of the General Relativity story. It was written by the great Freddie Mercury for Queen’s 1975 album, “A Night at the Opera.” As we shall see in our next installment, Mercury (the planet) plays an important role in bringing the importance of General Relativity to the attention of the scientific community, just like Mercury (Freddie) helped me explain it here. 🙂

PPS: This week I couldn’t capture all of this in one 3 minute video, so I tried to do it in two.

—————————————

This post is part of an ongoing series written for the General Relativity Centennial, celebrating 100 years of gravity (1915-2015).  You can find the first post in the series, with links to the successive posts in this series here: http://wp.me/p19G0g-ru.

Gravity 2: The Road to General Relativity

by Shane L. Larson

Science is, to some extent, a skill set that can be learned. Like playing piano or solving Rubik’s cubes or cooking Belgian cuisine. Using scientific thinking and applying it to the world is in large part a matter of practice and relentless dedication to getting better. But like all artforms, there is a small element of je ne sais quoi to it as well — a hidden reservoir of intuition and stupendous insight that is unleashed only sometimes.

Apple once had an ad campaign built around the mantra, “Think Different” (grammarians, hold your tongues, and your “ly”s and follow the mantra!). There were images of famous thinkers through the ages who approached the world differently than the rest of us. One of those was Albert Einstein.

Among a community of bright and creative people, it gives me pause to consider those people that we all think of as being remarkable. Albert Einstein is arguably the most famous scientist in history of the world, commanding the respect not just of the general populous, who have grown up immersed in his legend, but also the respect of the scientific community. Why is that? My colleague Rai Weiss, now an emeritus professor at MIT, recently noted that it wasn’t just that Einstein was smart, it was that he exhibited tremendous intuition. His great ability was to look at the same world the rest of us look at every day, and think different.

When Einstein began his quest to refine our understanding of gravity, he knew he was going to have to “think different” — this was, after all, what had led to special relativity in the first place! One of the earliest musings on the road to general relativity was a simple question: how do you know if gravity is pulling on you?

Everything I need to start developing some new ideas about gravity!

It’s a seemingly simple question, but it led to an interesting thought experiment. Imagine you and I are each in a small, windowless room with nothing but an apple and our smartphones (so we can text each other the results of the experiment I am about to describe).

Each of us drops our apple, and we see that it accelerates downward — it falls!  The apple starts from rest (at our hands) and speeds up as it falls toward the floor of our small room.  We excitedly text the result to each other and tweet pictures of apples on floors. Should we conclude from these experiments that we are both conducting experiments under the influence of a gravitational field?

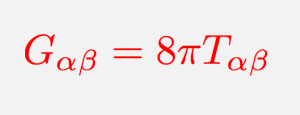
[Top] You and I conduct identical experiments (dropping apples) in enclosed spaces and get identical results. [BOTTOM] The reality of what is outside our little rooms may be completely different! A falling apple is equally well explained by the gravity of a planet, or by an accelerating rocket!

Einstein realized the answer to that question should be “No!” There are multiple ways to explain what we saw.  One way is to assume our little rooms are sitting on the surface of planet Earth, where the planet’s gravity pulled the apple down. But another, equally valid way to explain this experiment is to assume the little rooms are really the space capsules of rocket ships, accelerating through empty space (the apple is pressed down to the floor — “falls” — the same way you are pressed back in your seat when a jetliner takes off).  What Einstein realized is that there is no way, based on our experimental results, to tell the difference between these two cases. As far as experiment is concerned, there is no fundamental difference — that is to say, no observational difference — between them. Einstein knew that the laws of physics had to capture this somehow.

[TOP] You and I both find ourselves weightless, floating without feeling forces acting on us. [BOTTOM] The reality external to our rooms could be that we are floating in space, or that we are in a freely falling elevator plummeting to our doom.

What if we consider a slightly different case? Imagine you and I both suddenly found ourselves and our apples drifting weightlessly in the middle of our small rooms. We excitedly text each other that we finally made it to space and tweet messages that we are officially astronauts. Should we conclude that we are both deep in interplanetary space, far from the gravitational influence of a planet? Once again, Einstein realized the answer to that question should be “No!” There is no way to know if we are drifting inside a space capsule in deep space, or if we are merely inhabiting an elevator whose cable has snapped and we are plummeting downward toward our doom!

It is this freefall experiment that really illustrates how we have to learn to “think different” when expanding our understanding of Nature. In Newtonian gravity, we always look at problems with an exterior, omniscient eye toward the problem. A Newtonian approach to the free fall problem says “Of course you are falling under the influence of gravity! I can see the Earth pulling you down from the top of the skyscraper toward your doom at the bottom of the elevator shaft!” But Einstein asked a different question: What does the person in the elevator know? What experiments can they do to detect they are in a gravitational field? The answer is “none.”  There is no observational difference between these two situations, and the laws of physics should capture that.

The critical point here is that if you are in free fall, you feel no force! Einstein’s great insight was that the central difficulty with gravitational theory up to that point was that it was anchored in thinking about forces. This thought experiment convinced him that the right thing to think about was not force, but the motion of things.

This thought experiment came to Einstein in 1907 on a languid afternoon in the Bern patent office. Later in his life, Einstein would recall that moment and this idea with great fondness, referring to it as the happiest thought of his life.  This experiment is known as the “universality of free fall,” which physicists like to give the moniker “the Equivalence Principle.”

This is how I often imagine Einstein’s life during the years he worked in the Bern patent office! [From “The Far Side” by Gary Larson]

I have a very strong memory of my father first telling me about the universality of free-fall in about fifth or sixth grade. When you’re not used to it, the notion that falling in an elevator is the same as floating in outer space engenders a spontaneous and vehement response: “That can’t be true!” We had many long debates about this (it was following hot on the heels of my meltdown over the existence of negative numbers — maybe my dad was trying to forestall another meltdown…), and I don’t think it ever quite sank in. I, of course, feigned understanding and dutifully repeated the tale of the falling elevator to my classmates, reveling in their confusion and indignant denial of the logic of it.  I was a tween — what did you expect?

The “Leaning Tower of Niles,” a half-scale replica of the tower in PIsa. Located in Niles, IL (a suburb of Chicago).

But now, many years later and with a LOT of physics under my belt, I know that that the outcome of these thought experiments derive from a very old result that we are all familiar with — that all objects fall identically, irrespective of their mass. Galileo taught that, at least in folklore, by dropping various masses off of the Leaning Tower of Pisa. The obvious question to ask is “how is Galileo’s experiment connected to Einstein’s thought experiments?”

For the moment, imagine the various parts of your body as having different masses.  Your head masses about 5 kg (a little bit more than the 8 pounds you learned from watching Jerry Maguire), where as a good pair of running shoes may mass about 1.5 kg.  If you are standing happily in the elevator when the cable snaps, the traditional explanation is that everything begins to fall.

If objects of different mass fell at different rates, then your head would be pulled down faster than your shoes — you would feel a force between your head and your shoes. That force could be used to deduce the existence of a pulling force.  But Galileo taught us that is not the way gravity works — your head and your shoes will get pulled down at strictly the same rate in a uniform gravitational field. Every little piece of you, from your head to your toes, your kneecaps to your freckles, falls at the same rate — there are no different forces between the different parts of your body and so you feel (you observe) yourself to be weightless. This is sometimes called the Galilean Principle of Equivalence, or the Weak Equivalence Principle.

Okay — so what? Apples and freefall, elevators and rockets. What does any of this have to do with developing a deeper understanding of gravity?

What this thought experiment reveals, what the Equivalence Principle tells us, is that thinking about forces is not the best way to think about the world because we can’t always be sure of what is going on! Instead, we should think about what we can observe — how particles move — and ways to describe that. That simple intuitive leap would, in the end, change the face of gravity. Particles move through space and time, which had brilliantly been unified by Einstein’s teacher and colleague, Hermann Minkowski, into a single unified medium called “spacetime.”

What is spacetime? It is the fabric of the Cosmos —  it can be stretched and deformed. The fundamental idea of general relativity is that gravity can be described not by a force, but by the curvature of spacetime, the medium on which particles move.  That will be the subject of our next little chat.

—————————————

This post is part of an ongoing series written for the General Relativity Centennial, celebrating 100 years of gravity (1915-2015).  You can find the first post in the series, with links to the successive posts in this series here: http://wp.me/p19G0g-ru

Scientific Selfies

by Shane L. Larson

One of the great pleasures of my life is going to scientific conferences. I love sitting through talks, listening to my colleagues weave tales of things I’ve never thought about before. I find something deeply relaxing about simply letting new information seep into my brain and connect to things one might never have expected. It makes my life and daydreams interesting.

A favorite picture of Swiss astronomer, Fritz Zwicky.

I was sitting at a meeting in Denver recently, listening to one of my colleagues spin a tale I’ve heard before, about the dark matter in the Cosmos. The idea that the Universe is not entirely made of the same stuff as you and I was pioneered in the 1930s by Swiss astronomer Fritz Zwicky, based on a famous observation of the motion in a distant cluster of galaxies known as the Coma Cluster. Zwicky showed that if you count up all the stuff you could see in your telescope and compared it to how much stuff you need to make the galaxies move, there was some matter that was missing, or dark! This is a famous and important result, and my colleague did what we all do when we tell this tale: he put up a picture of Zwicky. More often than not, we all use the picture shown to the left!

Which got me to wondering — if Zwicky were still with us today (sadly, he has gone back to the Cosmos in 1974) and I were to drop him an email asking for a picture of him to show in a talk, what would he send me?

One of the most famous pictures of Einstein, taken on his 72nd birthday.

There are other examples of funny scientist pictures that are commonly used. Perhaps the most famous is of Albert “Big Al” Einstein, sticking out his tongue. The picture was taken by a UPI reporter on Einstein’s 72nd birthday, and was a favorite of Einstein’s. It is arguably one of the most popular images of Einstein and is used in many venues, especially when talking about complicated physical concepts that derive from Einstein’s work. I use it in two different instances. The first is when I’m trying to convince people that scientists aren’t completely serious people — we like to have fun and goof off; if Einstein did it, so can we! We’re people too! The second is when I’m talking to people about dark energy — a completely unknown physical effect that appears to comprise almost 70 percent of the Universe. Einstein’s famous “blunder,” known as the Cosmological Constant, is a leading candidate for explaining the dark energy. I like to think that if I could call Einstein up on the phone and tell him we were going to use his greatest blunder to explain the greatest mystery in physics today, he might think I was pulling his leg and blow a big raspberry over the phone, like he appears to be doing in this picture!

Not all of my colleagues use pictures when they talk science; not all of them regale us with historical tales of the subject they are outlining. But I always do because to me, the context of the story is as important as the scientific result itself. Science is a uniquely human endeavour — no other species that we know of studies the world like we do. Science, like art, is an intense expression of our innermost creativity and imagination. As such, it is important to me to put a human face on all the great mysteries we have unravelled, and on all the puzzles we are still trying to find answers to.

Consider Jane Goodall, widely known for her decades long research on the Gombe chimpanzees in Tanzania. I would love to be a collaborator with Goodall, so I could ping her for a picture to use. What picture would she choose? There are thousands of pictures of Goodall and the Gombe chimpanzees, many quite famous, but the most striking to me has always been this one by Michael Nichols of National Geographic. It captures so eloquently the interspecies interaction which has always been the hallmark of Goodall’s work. While the unconventional methods Goodall used in characterizing her work has often garnered criticism centered around the anthropomorphization of the chimpanzees, it is precisely the idea that we are closely related to these other Earthlings that makes Goodall and her work so compelling to the rest of us. All the subtle mix of wonder and mystery at this deep connection with our cousins, the great apes, is captured for me in this single image.

One of my favorite pictures of Jane Goodall (photo by Michael Nichols).

The existence of funny or striking images is largely due to the development and commercialization of film. Today especially, pictures are cheap and easy — goofing off for the camera is a worldwide pastime! But before cameras and photography became common, photographic pictures were posed and planned. As a result, as one looks back in time, it seems to me that we often simply have the image of famous scientists, and little of their personality. But I still show their pictures.

James Clerk Maxwell with his wife Katherine, and an unidentified sheep dog. 🙂

This is one of my favorite pictures of James Clerk Maxwell, though it is not one you often see. It shows the iconic Maxwell that is so well known to physicists, in his mid-life, with his signature bushy beard, together with his wife Katherine. Maxwell was a phenomenal physicist, contributing to many areas including color photography and thermodynamics. What he is most well known for, however, is the combination of electricity and magnetism into one, unified description of Nature now called “electromagnetism.” It was the first time humans had ever come to the realization that there was some deep unification possible in the Laws of Nature, and set the stage for fundamental physics research that continues to this day; the quest to find the Higgs boson is the distant descendant of Maxwell’s original epiphany about unification. What I love most about this picture is that Maxwell had a fuzzy sheep dog! If Maxwell had posted this picture to Instagram, I’m sure I’d shoot him a text right away saying, “LOL Jim. What’s the dog’s name?”

Portrait of a man in red chalk. Possibly a self-portrait of Leonardo da Vinci.

Beyond the horizon in time when photography was invented, our memories of distant ancestors and figures is reduced to art. It is no secret that I harbor a deep romanticism for Leonardo da Vinci, perhaps the greatest polymath known in history. It is a fond daydream of mine to imagine sitting on a hillside somewhere with Leonardo, sketching in my Moleskine next to the great master as we engage in idle chit-chat, speculating on the awesome machinery of Nature and how we humans might tap into that machinery and be more than we think ourselves to be — to fly, or traverse the wide oceans, or to build a violin whose sound would make the masses weep with joy to hear the sound of it. There are many portraits of Leonardo, but the one I carry in my mind is one that is thought to be a self-portrait (though this is debated), the famed “Portrait of a man in red chalk.” If it is Leonardo, it shows him late in his life. I’m most captivated by the eyes in this portrait — deep, hidden under bushy eyebrows, the corners lined with wrinkles that I imagine must be derived from a life filled with laughter and delight at all the world has to offer. Too much to read into fading lines of chalk sketched five hundred years ago? Perhaps, but it keeps me putting my pen to paper every day, spilling out crazy ideas and imaginings about the world. What would Leonardo do?

Because I do place great stock in the human story of science, my passion for showing pictures of scientists doesn’t end with historical retrospectives. Most of my colleagues have at some point in our collaborations been asked for a picture, so I can show the world the people I work with. They are all brilliant, unique, imaginative scientific minds. As you might imagine, their pictures reflect their inner brilliance. I show their pictures when I give talks to bring those human dimensions to our work, because I am proud to call them friends and colleagues.

Some of my collaborators, in self-chosen portraits.

Here is my academic family, my research group from my last year at Utah State University. They are, each of them, singularly brilliant and talented. Every one of them is just beginning to write their stories. I have no doubt that if they come visit me in the old scientists’ home when I’m 107, they’ll bring pictures of their adventures and tell me tales of the paths they walked in the world, no matter what they might be. We’ll pull out this old picture, and laugh at how young we all were back then, and how quaint “digital pictures” were back when that technology was new-fangled.

My academic family, in self-chosen portraits.

My scientific selfie. 🙂

Someday, one of my students, or one of you, will need a picture of me for something. When you do, do me a favor — no serious pictures. If I’m lucky, I’ll have some odd little picture that is so awesome everyone will use it, just like the picture of Fritz Zwicky. Until then, I’ll leave you with one my favorites — my selfie. Not as compelling as Goodall’s picture, nor as elegant as Leonardo’s portrait, but maybe as serious as Einstein’s. 🙂

A Rant Among Friends

by Shane L. Larson

<rant>

When you grow up and get a job, there is inevitably a Saturday night when you are talking on the phone with your mom, or enjoying a glass of Chianti with your date, and you have to answer The Question: “So what exactly is your job?” Then you fumble around for a few minutes trying to explain actuarial tables, or managing the supply line for a 7-11, or what a Toyota service manager actually does. Most careers are not reducible to a simple, one sentence sound bite understandable to relatives or members of the opposite sex. Almost certainly every job has different parts and pieces, each of which are worthy of their own sound bite!  If you love your job, then you want it sound exciting and sexy; you want your sound bite to be a sales pitch that might convince someone else to join your profession.

What’s in the Fear Closet?

As scientists, in particular scientists who are also university professors, my colleagues and I spend a lot of brain power thinking about this last part — how do you make sure people adopt science as a profession? I’m not yet besectacled and grey; my hair hasn’t yet gone the way of Big Al Einstein’s, so maybe I don’t yet have the wisdom (cynicism?) of my more elderly colleagues.  But late at night, when the world is slumbering and my grading is done, I like to open the Fear Closet in the back of my mind. Very seldom are Mike and Sully there to greet me; instead I usually find a big elephant that we scientists like to ignore: we often suck at making our profession appealing to anyone. Furthermore, we have an idealized model of who makes a good scientist that, like an unrealisticly proportioned Barbie doll, is not a good approximation of any person (or scientist) I know. The fears in the Closet all add up to one inescapable possibility: that like the dinosaurs of yore, who never became intelligent enough to save their race from impending doom, scientists could become extinct.

I’m a bit worried about the radio astronomers...

Now I don’t think that is a realistic fear; there are always going to be scientists.  But the landscape of our modern civilization is such that if scientists don’t evolve, we will become relegated to the backwaters of our society, currently occupied by mimes, disco, and Elvis impersonators.

This door of the Fear Closet has been open a lot lately, because scientists have an annoying habit of thinking they know everything, which means we (the scientists) think we know how to make other people love and revere science. I’ve been staring into the Closet with this in mind, and thinking back to my high school consumer affairs class where I was taught the Very Important Lesson: customers have all the power, because they have the choice to spend their money on your product or not.  If the consumers hate your product, they won’t buy it, and your business will fold. If the way you do business becomes obsolete, you won’t have any customers, and again your business will fold. Do you still have a Blockbuster down the street from your house? How about any product from Kodak? Maybe you still watch the XFL?  No? These ventures all failed to respond to the external demands placed on them by their consumer base; they failed to evolve.

Some notable examples of failing to evolve in response to customer needs and desires. Recognize any of these?

This must be true in science too — if people don’t like the way we present and promote and sell science, they will ignore us.  An interesting case study on this point is a very pointed article a colleague of mine linked to the other day, written by Maura Charette (an eighth grader!), reflecting on STEM (Science, Technology, Engineering and Mathematics) careers (link to article).

Ms. Charette’s essay is brilliant, and as STEM professionals we should take many of her points to heart. I don’t disagree with anything she says.  But in the interest of inciting discussion, why don’t I summarize what I took away from the article (for future reference, when examining the contents of the Fear Closet):

(0) Ms. Charette writes, “while we hear science and math careers are fun, interesting, and well-paying, the actual scientists and engineers who visit our schools seem very one-dimensional.”  Despite the ascendance of geekdom into the mainstream of popular culture, scientists still maintain a stranglehold on being the opposite of cool; we are the George MacFly’s of the geeks. Not to say that there aren’t superstars among us — the public adores Neil deGrasse Tyson and Bill Nye. People like Brian Greene and Lisa Randall are at least commonly known names in some circles.  But the vast majority of us exude the exact opposite of what we want to inspire — excitement and fun.  We are, as Ms. Charette so aptly observes, one dimensional. Now it is not possible, nor desireable, for all of us to become great public personalities. But what we must stop doing is discouraging, disdaining, and ostracizing our colleagues who are good at this. Elitism abounds in science; we place far more value (as a group) on the trappings of science — research, discovery, appearing smart — than we do on the interfaces with science — teaching, writing, communicating. Many of those who act in the interface roles are not afforded the same encouragement or respect as those who act in the “popular” roles (this is in fact, a common occurrence in all academic fields, particularly at universities).  Communicating our science to the society that funds (and tolerates) us is as noble a cause as any bench science you care to name, and as it turns out, just as important.

(1) Let’s be blunt — we don’t make science exciting. If I may be a bit bold and exhibit one of the annoying traits of adults, let me rephrase Ms. Charette’s message in my own words (a classic classroom exercise!): scientists suck. Particularly at teaching.  Not all of us; many of us are great teachers (my colleagues at Weber State University Physics come to mind).  But all too often what we teach lacks the fire, the passion, the core of what drew every one of us into the field.

How we teach adversely affects opinions about our craft. We need to consider perspectives that draw people into what we want them to know…

Why did YOU get into science?  I got into science because black holes are freakin’ AWESOME (and pretty much every 9 year old on the planet agrees with me). When I lay awake at night, staring at the patterns of light on my bedroom ceiling and thinking about black holes, I don’t push tensors around in my head and think about geodesic deviation and metric functions. I think about black holes tearing stars apart; I think of black holes lying in wait at the bottom of the galactic core, waiting to suck up unsuspecting stars and gas clouds.  These are the things to talk to people about and to teach about.  The technical matters are important — no doubt about it — but what people need is that deep seated sense of wonder about the world around them that makes them lay awake at night pondering how high grasshoppers jump compared to their body length, and why the Great Lakes don’t have huge tides like the ocean, and how long it will take the Rocky Mountains to wear down into sad little nubbins like the Appalachians.  You and I stay in science for those reasons, for the wonder of it. We’ve learned the technical tools, and we use them to illuminate the world and make our understanding more remarkable and enjoyable.  But we didn’t come to science because of the technical stuff.  Teach to the passions that draw people.

(2) Scientists place an over-emphasis on good grades. One of the most disturbing things (to me) that Ms. Charette wrote is this: “to pursue and succeed in those one-dimensional jobs, you have to study very hard and get good grades in the most difficult subjects.”  As near as I can tell, someone in eighth grade is already considering giving up on science because of grades.  Getting good grades is the conventional folklore, which scientists loudly advocate, and it makes me want to puke at night worrying about how many kids we drive away from science because of it.  Does having good grades help be a good STEM professional? Of course it does, but it is no substitute for hard work and a good work ethic.  Some of the people I know with the most flawless report cards in math and science SUCK at being a STEM professional!  Why? Because they are good at doing homework, finding out the “right” answer using well known conventional thinking.  But they completely lack any creativity, imagination, intuition, or ability to make brilliant leaps of logic that are so crucial to making important advances in science.

(2.5) Just to prove you don’t need good grades to be a successful scientist, let me bare my soul to the flames of the Internet. I got a C in thermal physics as an undergraduate.  I took Calculus II twice (on purpose) because I didn’t understand it the first time; the second time I decided I wasn’t meant to understand integration by parts and moved on (and I still can’t recognize when to do it). I got a LOT of B’s (and at least one C), and only a handful of A’s in graduate physics.  After my first year of graduate school, the department head in Physics called me into his office and told me I didn’t have a future in science, and I should drop out and go do something else with my life.  To encourage me to see the world his way, he didn’t provide any summer support for me (but did for the rest of my classmates). I ignored him, of course. That summer I went out and found another job and met two of the great scientific mentors in my life (Dr. Kimberly Obbink, and Dr. Gerry Wheeler). I finished my courses, and I completed my Ph.D. without difficulty. In the years since, I like to think that I’ve been a reasonably successful scientist by most of the measures of my professional community.  I had postdocs at some of the best institutions in the world (JPL, Caltech, and Penn State); I’m a tenured professor; I have 50 some-odd publications; I’ve successfully acquired multiple federal grants to support my students and my research; I was “Professor of the Year” one year.  CLEARLY he was right; you have to have perfect grades to be a good scientist. WTF was I thinking?!

My fort!

(3) Lastly, let’s review the title of Ms. Charette’s essay: “Is a Career in STEM Really for Me?” Really?  Have we stooped to the point where 8th graders have to be cognizant and concerned with their careers?  In 8th grade I was 13; I didn’t enter graduate school until I was 21 and I didn’t get my PhD until I was 29.  When I was 13, I wanted to be an astronaut, not a relativistic gravitational astrophysicist. When I was that age, I didn’t worry about careers yet; I was BUILDING FORTS!  If you look at my fort, it is clear that there was some STEM in there — obviously some math, as well as some attempts at engineering. 🙂  I was doing “STEMy” kinds of things (as were both my brothers — one is now a diesel mechanic, the other a crop scientist — both STEM professionals).  We know that middle school years are the years where kids lose interest in science, but making them think about STEM careers is NOT the way to keep them engaged!  Neither are marshmallows and straws.  Kids are smart, intelligent, and capable. They live in a world filled with modern marvels that are commonplace to them: smartphones, streaming digital media, microwave popcorn. We need to field science that is engaging enough to compete in that marketplace and we need to do it sooner rather than later (just ask Blockbuster and Kodak how easy it was to catch up…).

Me and Xeno.

So what to do about all of this?  My mother taught me that one cannot simply complain about the world without offering solutions. Be a problem solver, not a trouble maker. Yes, Ma; I remember.  I’m just not sure what to do about it yet; I promise to work on this.

My therapist (Xeno) says ranting is not good for my blood pressure, so I’ll stop now.  But if you have any great ideas, by all means let me buy you a beer and a pizza so we can figure out what to do next!

</rant>

Gravity does the talking

by Shane L. Larson

Obi-wan Kenobi, in perhaps one of the most famous utterances in cinematic history, claimed that the Force “is an energy field, created by all living things. It surrounds us, it penetrates us, it binds the galaxy together.” This propagated rapidly through popular culture when it was realized that Obi-wan must have been talking about duct tape, which after all has a light side, a dark side, and also binds our world together.

The famous utterance of Ben Kenobi’s description of the Force (from “Star Wars”).

But an astute citizen of the Cosmos may grow curious at Kenobi’s observation, and ask “what does bind the galaxy together?” As it turns out there is a force that penetrates the fabric of the Universe, in a way it is the fabric of the Universe. We call it gravity.

Many of us have heard the idea that there are four fundamental forces in Nature: gravity, the electromagnetic force, the weak nuclear force, and the color force (the “strong nuclear force” is a faint bit of the color force that “leaks” out of atomic nuclei to be detectable by our experiments). Why is gravity The Force? Why not the others?

The four fundamental forces of Nature emerged after the Big Bang, as the Universe cooled and expanded.

In order to fill the Cosmos, a force must be a long range force — the Cosmos is a BIG place!  The weak nuclear force and the color force are short range — they act very strongly over very tiny distances, in atomic nuclei and in the nuclear particles that comprise nuclei. The electromagnetic force is a long range force, but it acts in the presence of electrically charged particles, which come in two flavors — positive (+) and negative (-). It is easy to make separate positive and negative charges and to locally generate strong electromagnetic forces (lightning is a prime example from Nature), but by and large the Cosmos is electrically neutral — opposite charges are attracted to each other, and they quickly neutralize and cancel each other out, leaving no free charge behind.  Gravity is also a long range force, but it has only one kind of “charge,” which we call “mass.” There is no negative mass, so gravity cannot be shielded or canceled, and it acts over vast distances.

Gravity is the only game in town when it comes to forces acting on cosmic scales, despite being so incredibly weak.  I can see the skepticism on your face!  I said gravity binds the Cosmos together, and in the same breath said it was incredibly weak!  Whatever do I mean?

I tried as hard as I could to break the apple in two!

I mean that gravity is weak compared to the other forces of Nature, a fact you can easily demonstrate in your kitchen. Pick up an apple.  What is holding an apple together?  It is mostly intermolecular forces between the molecules that make the apple up, and those forces are electromagnetic in nature.  Now,using your bare hands, try to break the apple half.  Not so easy, is it?

Using the chemical energy from some Dr. Pepper, I can overcome the gravitational pull of the entire planet.

Now, stand up and jump up in the air. How high did you get? Even if it was just a couple of inches consider this fact: you were able to momentarily over come gravity.  Using a little bit of chemical energy, gleaned from that rabbit food you ate at lunch (perhaps an apple you ate), you were able to overcome the gravitational pull of the ENTIRE EARTH!  Gravity is weak (and you are strong).

While these kinds of deep machinations are fascinating questions into the deep nature of Nature, you might still be scratching your head wondering what good is this knowledge? The first widely understood law of Gravity was Newtonian gravity, described by Isaac Newton in 1687.  It was used almost immediately to begin describing the motion of heavenly bodies, but by and large the world went about its business more or less oblivious to this stunning achievement of the human intellect.  The practical application of Newtonian gravity, using it for something that humans build or use, was not for almost 270 years: in 1957, the Soviet Union launched Sputnik, requiring a detailed understanding of orbital dynamics, which is derived from Newtonian gravity.  By a similar token, Albert Einstein wrote down the modern description of gravity, general relativity, in 1915. There were immediate applications of general relativity to astrophysics (a trend that has only grown since), but practical applications to human affairs did not seriously arise until the late Twentieth Century.  Let me tell you some stories about how gravity, general relativity, is changing our world.

GRACE.  Our society is engaged in much teeth-gnashing about the nature of the Earth’s changing climate, but most scientists are doing what scientists do best — they put their heads down, they collect data, then they figure out what the data is telling them.  Of particular importance to climate studies is the hydrological cycle on Earth.  Gram for gram, water is a bigger player in thermodynamics than any other substance on Earth. It is extremely effective at cooling and heating, which is why you use it to cool off in the summer and warm up in the winter!  The movement of water on Earth, in the oceans, the clouds, the rivers, and the atmosphere has enormous impacts on climate worldwide.  But the hydrosphere is HUGE! We can’t possibly hope to monitor water levels and water flow in lakes and rivers and oceans worldwide by placing individual sensors.  So how are we to learn about the water on Earth and how it moves and changes?  The answer is we use gravity.

(L) Satellite geodesey monitors the orbit of a satellite to understand the underlying source of gravity. (R) The GRACE geodesey system uses two satellites keeping track of each other using a microwave link.

Satellite geodesey can make precision measurements of the Earth’s gravitational field. As a satellite flies over the Earth, the changing mass below the satellite changes the strength of gravity, which alters the satellite’s trajectory in its orbit.  We monitor the orbit to know how the gravity (and the mass creating the gravity) is changing!  In 2002, NASA launched a mission called GRACE (Gravity Recovery and Climate Experiment), consisting of two satellites flying about 220 km apart, monitoring each others’ orbit using a microwave signal.  For over 5 years, GRACE monitored the Earth’s gravitational field and was able to see how it changes as water and ice move around our planet.  Just one example is shown below, illustrating how the gravity in the Amazon basin goes up and down with the coming and going of the rainy season.  Similar results illustrate the changing ice around the planet, particularly in the Arctic and Antarctic.

GRACE geodesey is sensitive enough to detect the change in gravity over the Amazon basin as the rainy season comes and goes.

GPS.  Perhaps the most ubiquitous use of gravity in your everyday life is the global positioning system. Once relegated to navigation on planes and automobiles, the advent of GPS built into smartphones has enabled an explosion of location services that allows you to find friends, local restaurants, comic book stores, and concert venues in unfamiliar cities.

Fundamentally, GPS works by triangulation.  Satellites send out timing signals that are received by your smartphone or GPS navigator. The signals are broadcast in synch with one another. This means that if you are an equal, fixed distance from two satellites, you’ll get the same time from both (this is like using headphones — the sound from the L and R side are synchronized so you hear all the right parts of the song and the same time!).  If you are closer to one satellite, then you receive a time from that satellite sooner than a distant satellite (this is like watching a track meet from the stadium — runners hear the starting gun before you do, because they are closer).  Your navigator compares your local time to the time received from the satellites, allowing the determination of distance to each satellite. Since the position of each satellite is known, your location can be computed.

GPS triangulates your location by comparing the received time from multiple satellites.

The satellite timing signals must be modified, using general relativity.  Why?  The satellites are much higher in the Earth’s gravitational field than you are, and general relativity tells us their clocks tick at a different speed. How much different? Over the course of a day, the general relativity correction to the clock times is about 38 microseconds — 38 millionths of a second!  You may be thinking “But that is so tiny!”  Yes it is tiny, but GPS works based on how far light travels in a given time.  In 38 microseconds, light travels 11.4 kilometers (7 miles)!  When you are trying to find a sushi restaurant, or the soccer field for your kids next game, 11 kilometers is a long way off!

Gravitational waves. Let me tell you one last story, not about the practical uses of gravity, but about our dream of using gravity to reveal the secrets of the Cosmos.  In 1918, while exploring the implications of general relativity, Einstein discovered that there exists a kind of gravitational radiation, where the gravity from an astrophysical system carries energy away and into the far reaches of the Universe.  He calculated the strength of this radiation, and very quickly decided that it would be exceedingly difficult (if not impossible) to experimentally measure.

But fast-forward the blu-ray to today, and we have technology at our disposal that Einstein could never have imagined — high precision, high power lasers; GPS positioning systems to accurately locate anything anywhere on the planet; high performance computers capable of performing billions of computations per second; a globe girdling network that passes information from one continent to another as easily as one might shout down the hallway to a colleague; and most importantly, a vast community of scientists well-trained and well-versed in wresting secrets from Nature, the best minds our planet has to offer. You add that all together, and we find ourselves in the land of Einstein’s dreams, poised to measure the faint echoes of gravity bathing the Earth from distant corners of the Cosmos.

Nearly a century of thinking on the matter of gravitational radiation has coalesced around a magnificent machine called LIGO — the Laser Interferometer Gravitational-wave Observatory.  Using lasers shining up and down 4 kilometer long beam arms, a new generation of astronomers — gravitational wave astronomers — hope to detect the dance of neutron stars and black holes spiralling toward collision, the constant drone of young pulsars spinning down into their final rest in the stellar graveyard, and maybe (if we are lucky) the cataclysmic supernova explosion of a star dying, a process that synthesizes most of the atoms that comprise what we are all made of.

The LIGO Observatory at Livingston, LA. There is a companion observatory in Hanford, WA.

Gravitational wave astronomy is a way of asking anew the questions about who we are and what our place in the Cosmos is; it is a way of once again indulging in the unique gift to our species, an insatiable sense of curiosity and wonder.  But are there practical outcomes from this remarkable feat of human imagination? Perhaps not obvious ones, because the practical outcomes were not the driving force in the creation of the experiment. But as with all great feats of science and engineering, from the Manhattan Project to Apollo to LIGO, there are always beneficial outcomes.  Already LIGO’s technology is pushing the frontiers of optics and laser technology, environmental monitoring, and computer network capabilities.  But changes you see in your living room may be 7 or 70 or 270 years away.

This has always been the case for gravity; the timescale is simply a matter of how creative our engineers and scientists get!

In Living Color

by Shane L. Larson

I don’t often talk to people for great lengths of time on airplanes. I’m kind of shy around people I don’t know.  But on a recent long flight home from the East Coast, I found myself sitting next to a wonderful woman, 75 years young, and we talked for the entire 5 hour flight.  Stefi was a gold- and silversmith from Vermont, and a German immigrant.  Our conversation ranged from the art of jewelry making, to winters in Vermont, to her grandchildren whom she was going to visit in Utah.

But at some point, the conversation strayed to her childhood in Berlin, where she lived as a young girl during the closing days of World War II.  There, sitting right next to me on the plane, was a living, breathing soul who had lived through the heart of World War II.  Not a soldier, not a support person who worked the fronts or factory lines, but a person caught in the middle of the war itself. From vivid memory, she recounted tales of what she saw, living huddled in a basement with her mother and sisters as the end of the War approached.  She was there as the Red Army advanced toward the Battle of Berlin, and saw the Russian occupation of the city.  In her mind’s eye, she could see it all in living color again.  But my vision was only pale black and white; the only images of the War that anyone in my generation has ever seen are stark black and white images.

In the days after the flight, long after Stefi and I had gone back to our respective lives, I was thinking about the differences between memory and historical record. In physics, we have similar historical records of our distant past, also preserved in stark, black and white images.  One of the most famous images in my field, is of the Fifth Solvay Conference on Electrons and Photons, held in the city of Brussels in October of 1927.  The reason this particular conference is so well known is the iconic black and white photograph captured of the participants.

The participants in the 1927 Solvay Conference on Electrons and Photons, in Brussels.

Scanning through the photograph, or running your finger down a list of names, one encounters names that are completely synonymous with the development of modern physics. Of the 29 participants, 17 went on to win Nobel Prizes; included among them is Marie Curie, the only person who has ever won two Nobel Prizes in different scientific disciplines!  This single image captured almost all of the architects of modern physics.  These are the minds that seeded the genesis of our modern technological world.  The conference itself has passed into the folklore of our civilization, as this was the place that Einstein expressed his famous utterance, “God does not play dice!”  Neils Bohr famously replied, “Einstein, stop telling God what to do!”

For many of us in this game called physics, the people in this image are icons, idols, and inspirations.  We know their names, we know their stories, and we can pick them out of pictures as easily as we can pick friends out of modern pictures.  But always in the dull and muted grain of black and white photographs. I’ve never met a person (that I know of) that met Einstein, or Bohr, or Heisenberg, or Curie; no one to recount for me the vivid colors of these great minds in their living flesh.

It is an interesting fact that all of these historical images are black and white. Color photography was first demonstrated some 66 years earlier at the suggestion of another great mind in physics, James Clerk Maxwell.

The first color photograph ever taken, by Thomas Sutton in 1861 at the behest of James Clerk Maxwell. The image is of a tartan ribbon, captured by a three-color projection technique.

The process worked by taking three black and white pictures through colored filters — red, green and blue — then reprojecting the black and white pictures through the filters again to produce a colored image.  This is more or less the same principle that is used today to generate color on TV screens and computer monitors.  If you look very closely at the screen you are reading this on, you will see that the pixels are all combinations of red, green and blue.

An example of RGB image construction. The three black and white images on the left were taken through Red (top), Blue (middle) and Green (bottom) filters. When recombined through those colored filters, they produce a full color image (right).

The famous tartan picture was generated for a lecture on color that Maxwell was giving.  Maxwell’s interest in light and color derived from the reason he is famous  — Maxwell was the first person to understand that several different physical phenomena in electricity and magnetism are linked together.  His unification of the two is called electromagnetism.  One consequence of that unification was the discovery that the agent of electromagnetic phenomena is light.  Today, the four equations describing electromagnetism are called the Maxwell Equations.

As with all things in science, the elation of discovery is always accompanied by new mysteries and new questions. One of the central realizations of electromagnetism was that light is a wave, and that the properties of the wave (the wavelength, or the frequency) define what our eyes perceive as color.

The electromagnetic spectrum — light in all its varieties, illustrated in the many different ways that scientists describe the properties of a specific kind (or “color”) of light. What your eye can see is visible light, the small rainbow band in the middle.

The realization that the color of light could be defined by a measurable property was a tremendous leap forward in human understanding of the world around us, and it naturally led to the idea and discovery that there are “colors” of light that our eyes cannot see!  Those kinds of light have often familiar names — radio light, microwave light, infrared light, ultraviolet light, and x-ray light.  But knowing of the existence of a thing (“Look! Infrared light!”) and being able to measure its properties (“This radio wave has a wavelength of 21 centimeters.”) are not the same thing as knowing why something exists.  How Nature made all the different kinds of light and why, were mysteries that would not be solved until the early Twentieth Century, by many of the great minds who attended the Solvay Conference.

Einstein famously discovered the idea that there is a Universal speed limit — nothing can travel faster than the speed of light in the vacuum of space.  Max Planck postulated that on microscopic levels, energy is delivered in discreet packets called quanta — in the case of light, those quanta are called photons.  Neils Bohr used the Planck hypothesis to explain how atoms generate discrete spectral lines — a chromatic fingerprint that uniquely identify each of the individual atoms on the periodic table. Marie Curie investigated the nature of x-ray emission from uranium, and was the first to postulate that the x-rays came from the atoms themselves — this was a fundamental insight that went against the long held assumption that atoms were indivisible, leading to the first modern understandings of radioactivity.  Louis deBroglie came to the realization that on the scales of fundamental particles, objects can behave and both waves and particles — this “duality” of character highlights the strangeness of the quantum world and is far outside our normal everyday experiences on the scales of waffles, Volkswagens and house sparrows.  Erwin Schroedinger pushed the quantum hypothesis on very general grounds, developing a mathematical equation (which now bears his name) that gives us predictive power about the outcome of experiments on the scales of the atomic world — his famous gedanken experiment with a cat in a box with a vial of cyanide captures the mysterious differences in “knowledge” between the macroscopic and microscopic worlds.  And so on.

The visible light fingerprints (“atomic spectra”) of all the known chemical elements. Each atom emits and absorbs these unique sets of colors, making it possible to identify them.

It is fashionable in today’s political climate to question the usefulness of scientific investigations, and to ask what benefit (economic or otherwise) that basic research investment begets society. Looking at the picture of the Solvay participants and considering their contributions to the knowledge of civilization one very rapidly comes to the realization that their investigations changed the world; in a way, their contemplations made the world we know today.  The discovery of radiation led directly to radiological medicine, radiation sterilization, nuclear power, and nuclear weapons.  The behaviour of atoms and their interactions with one another to generate light leads to lasers, LED flashlights, cool running lights under your car or skateboard, and the pixels in the computer screen you are reading from at this very moment. The quantum mechanical beahviour of the microscopic world, and our ability to understand that behaviour leads directly to integrated circuits and every modern electronic device you have ever seen.  That more than anything else should knock your sense of timescales off kilter; at the time quantum mechanics was invented, computers were mechanical devices, and no one had ever imagined building a “chip.”  The first integrated circuit wasn’t invented until 1958, when Jack Kilby at Texas Instruments built the first working example, 31 years after the Solvay Conference; the first computer using integrated circuits that you could own didn’t appear until the 1970s, and smartphones showed up in the early 2000’s.  The economic powerhouses of Apple, Microsoft, Hewlett-Packard, Dell, and all the rest, are founded on basic research that was done in the 1920s and 1930s.

Which brings me back to where we started — pictures from those bygone days.  After the first tri-color image of Maxwell’s tartan, the development of color photography progressed slowly. The 1908 Nobel Prize in Physics was awarded for an early color emulsion for photography, but the first successful color film did not emerge until Kodak created their famous Kodachrome brand in 1935.  Even so, color photography was much more expensive than black and white photography, and was not widely adopted until the late 1950s.  As a result, our history is dominated by grainy, black and white images.

So it was a great surprise last week when the Solvay Conference picture passed by in one of my friend’s Facebook stream, in color!  Quite unexpectedly, it knocked my socks off. I spent a good long time just staring at it.  Never before had I known of the flash of blue in Marie Curie’s scarf, Einstein’s psychedelic tie, or Schroedinger’s red bow tie (is Pauli looking at that tie with envy?).  But more importantly, the people were in color, as plain as if they were sitting across the table from me. It’s a weird twist of psychology that that burst of color, soft skin tones of human flesh, suddenly made these icons all the more real to me.

Colorized version of the famous 1927 portrait of the Solvay Conference participants [colorized version by Sanna Dullaway].

No longer just names and grainy pictures from history books, but rather remarkable minds from our common scientific heritage, seen for the first time in living color by a generation of scientists long separated from them.