Gravity 04: Testing the New Gravity

by Shane L. Larson

In the world of artistic painting, connoisseurs have a word: pentimento. It is the revelation of something the artist hid from us.  There are many reasons why changes to a composition may come to light. Sometimes it is because as paint ages, it becomes more translucent, revealing a previous facial expression or position of a hand. Sometimes, close and careful study reveals that a slight alteration was made to disguise a mistake or a shift in ideas about the composition. And still sometimes technology can be used to see through the painting to what lies beneath — the artist’s original sketch or painting that was altered in the final production

The word pentimento is an Italian word, meaning “repentance.” Its use in the context of art is an implication that the artist has been caught red-handed, changing their mind about a particular composition! The idea of repentance and being caught red-handed carries a certain amount of emotional baggage in our culture; I suspect it is ingrained in us at an early age, when our parents catch us doing something we’d rather them not know — like stealing cookies from the cookie jar, or seeing what we look like if we cut our eyelashes off, or getting caught reading Scientific American under the covers with a flashlight (I just made all of those things up — my parents never caught me doing any of those!).

But science is different. Part of the game is about being wrong and getting caught. There is no shame in changing your mind, no repentance for previous incorrect speculations about the nature of the Cosmos. You make up cool ideas, that you present to the world not as art, but as proposed mathematical explanations for how the Cosmos works. Any crazy idea is fair game, with one requirement: you have to also suggest a way for us to do an experiment to test if your crazy idea is right! If it’s right, we go think of new experiments; if it is wrong, then we look at your crazy idea and figure out which crazy bits of it aren’t quite right. We make some changes, turning it into a new crazy idea, and then go conduct another test.

Science is always these two parts — the first part, describing the world, is called “theory”; the second part, testing your ideas, is called “experiment.”

The leading header of the paper where Einstein introduced general relativity, his writeup of the presentation he made to the Prussian Academy of Sciences in November, 1915.

Albert Einstein introduced General Relativity to the world in a presentation to the Prussian Academy of Sciences in November of 1915; his written summary of that presentation may be read (in German) online: Die Feldgleichungen der Gravitation (“The field equations of gravitation”).  If you look at that paper, you will see it looks a lot like your introductory physics textbook looked — lots of mathematical symbols and equations. What does it all mean?  This is the “theory” side of gravity, where we imagine the Laws of Nature that describe gravity — in this case, the idea that gravity can be explained as the curvature of spacetime.

General relativity was a tremendous step forward in our understanding of gravity — it was consistent with special relativity and extended our understanding into physical regimes that Newtonian gravity could not address. But at the same time, especially early on, very little was actually known about GR. It was mathematically difficult to work with (in the lingo of physics, it is “non-linear”), and in 1915 there were no known astrophysical systems that absolutely required general relativity to describe them. Einstein knew it was fine to write down new and possibly crazy ideas about the Universe, but the real task was to decide if there were ways to test those ideas. Were there some observations that could be made and compared against the predictions of general relativity? Observations that confirmed the predictions of general relativity would demonstrate its viability as a description of gravity. There have been many tests of general relativity discovered over the course of the past 100 years, but Einstein himself set the stage for testing his ideas by proposing three immediate tests that scientists could put their efforts into.

The first test was one that Einstein used to convince himself that general relativity was going in the right direction. In 1859 Urbain Le Verrier had noticed something odd about Mercury’s orbit.  Like all planets, Mercury has an elliptical orbit — it is a slightly squashed circle, closer to the Sun on one end than on the other. The point where the orbit comes closest to the sun is called perihelion, and it lies in a particular direction. Over time, the direction to perihelion changes — the orbit of Mercury pivots slowly, in a dance that astronomers call precession.

The point of closest approach to the Sun is called perihelion, and occurs in a certain direction (green dashed lines). Over time, an orbit pivots slowly — it precesses — changing the direction to perihelion.

Some precession is expected, because the Sun is not a perfect sphere (it is actually a bit squashed, fatter at the equator because it is spinning), but Le Verrier had looked at 150 years of observations of Mercury’s orbit and discovered the perihelion was shifting by an anomalously large amount — 43 arcseconds every century! That is to say, the angle of Mercury’s orbit was pivoting by an extra angle over the course of 100 years, equivalent to 43 arcseconds. How big is 43 arcseconds? Take a quarter and put it 382 feet away (a bit longer than a standard US football field) — 43 arcseconds is the angle between pointing from one side of the quarter to the other side of the quarter. It is a VERY small angle! But astronomers had detected this small change in Mercury’s behaviour through diligent and careful observations of the Cosmos.

43 arcseconds is about the apparent visual size of a US quarter when viewed from a distance of 382 feet (116.4 meters), slightly farther than the length of a regulation NFL football field.

When he was developing his new way of thinking about gravity, Einstein realized that the anomalous precession might be described by general relativity. He calculated that general relativity predicts an extra 43 arcseconds in perihelion precession for Mercury, the exact amount observed by astronomers. This not only resolved a 50 year old mystery in astronomy, but firmly convinced Einstein he was on the right track.

The second test is arguably one of the most famous tests in the history of gravity, and its success catapulted Einstein into the public eye, making him a world-wide celebrity. One of the central features of general relativity is that everything experiences gravity — everything “falls.” This is certainly true for things like rocks and slurpees, but Einstein also realized it should apply to light. Light, like all freely moving objects, wants to travel in a straight line, and generally it does so. This is one of the features that makes it such a useful messenger in astronomy: if you receive some light on Earth, and look back along the direction the light came from, you should be looking at the object that generated the light!

[A] When viewed alone in the sky, two stars (yellow and red) have a well defined separation, defined by the direction you have to point to look directly at them. [B] They appear separated, and that amount can be measured. [C] During a total solar eclipse, light from the yellow star passes near the Sun and is bent. Looking back along the line of sight, the yellow star appears to be closer to the red star than it was when the Sun was not in the way. [D] The deflection of starlight is the amount the position of the yellow star appears to move on the sky.

If on its long journey through the Cosmos a little bit of starlight (called a “photon”) passes near an object with strong gravity, the gravity will bend the path the light travels on. This is exactly what would happen to any massive object. If an asteroid is flying through deep space, it will travel in a straight line. If it strays too close to an object with strong gravity, like Jupiter or the Sun, the gravity deflects that asteroid and it ends up travelling in a different direction.

One of Eddington’s images recorded during the 1919 Eclipse. The small horizontal hash lines mark the stars that would be measured.

So how can you measure the bending of light predicted by general relativity? The trick with light is if you want to see the deflection, it has to pass through a strong gravitational field. Einstein suggested you could look for the deflection of starlight during a total solar eclipse. The gravity of the Sun is strong enough to bend the path of light by a measurable amount; during an eclipse when the Moon blocks most of the light from the Sun, the stars near the edge of the Sun’s disk should be visible.

The first realization of this test was organized in the United Kingdom by the Astronomer Royal, Frank Watson Dyson, and Arthur Stanley Eddington. Eddington led an expedition to the island of Príncipe, off the west coast of Africa, to observe the total solar eclipse on 29 May 1919. Eddington imaged several stars around the eclipse, and confirmed general relativity’s predictions. These measurements are difficult to make, and their accuracy has often been debated, but the experiment has been repeated during many eclipses since then, continuing to confirm the predictions of general relativity.

The leading header of the paper summarizing Eddington’s measurements to confirm the deflection of starlight.

The last proposed experiment is called the gravitational redshift. Think about tossing a rock up in the air. What happens? When the rock leaves your hand, it has some initial amount of energy that physicists call “kinetic energy” — energy associated with motion. As it climbs, it slows down. It looses kinetic energy, expending it to fight upward against gravity. Einstein argued based on the Equivalence Principle that a photon must also expend energy to climb upward against a gravitational field.

Photons travelling upward in a gravitational field lose energy, becoming redder. Photons travelling down gain energy, becoming bluer.

But photons — all photons — propagate at the speed of light! The notion of “kinetic energy” as it applies to objects like rocks is hard to extend to photons. But the Equivalence Principle demands that a photon climbing up through a gravitational field must give up energy. How? It can change its color. Photon energy is directly related to its color — blue light is more energetic than green light which is more energetic than red light.  A photon can give up energy as it climbs upward against gravity by changing its color, shifting from bluer light toward redder light.

Measuring the change in color of light is easy to do, but notoriously difficult to attribute to general relativity because all kinds of things change the color of light! But in 1959, Robert Pound and Glen Rebka successfully measured the gravitational redshift at the Jefferson Laboratory at Harvard.

Pound and Rebka’s triumphant measurement concluded a more than 40 year effort to complete the three classical tests proposed by Einstein in 1915. Since those early days, many other tests of general relativity have been suggested, and measured. To date, no experiment has uncovered any chinks or holes in the theory. If there had been, then general relativity would have been relegated to the trash bin of Cool Ideas that Failed, and we would have moved onward to look for a new understanding of gravity. Instead we find ourselves in that happy frame of mind where we use general relativity to describe the Cosmos with swagger and aplomb. There may yet be another revolution in our understanding of gravity, but if there is, I am confident that it will have to successfully include both general relativity and Newtonian gravity as parts of its core infrastructure.

In the end, there is a bit of pentimento in the game of science, but it is not on our part — it is Nature’s. General relativity is the latest in a series of tools that we have developed and used to peer closely at Nature. Slowly — ever so slowly — we are seeing through the paint Nature has clothed herself in. The secrets of the Cosmos are becoming slowly transparent, revealing the clockwork wonder of the Universe that hides beneath.

—————————————

This post is part of an ongoing series written for the General Relativity Centennial, celebrating 100 years of gravity (1915-2015).  You can find the first post in the series, with links to the successive posts in this series here: http://wp.me/p19G0g-ru.

Gravity 03: Curvature & the Landscape of the Cosmos

by Shane L. Larson

Had he been alive when Queen formed in 1970, perhaps Einstein might have jammed with them.

“Is this the real life? Is this just fantasy?”  So opens the classic rock song by Queen, Bohemian Rhapsody. Trying to understand modern gravity often puts one in the frame of mind that the mental machinations we go through are somehow not connected to reality. Albert Einstein’s genius was that he persevered through those uncomfortable feelings. He willfully ignored traditional ways of thinking about the real world, and imagined new and inventive ways to describe how Nature behaves.

One of those inventive ways of thinking was to noodle about unusual situations, like the Equivalence Principle. What a happy little thought — an idle daydream to imagine an elevator on the Earth, or flying in a rocket, and asking what would happen if you did something as simple as drop an apple? Dropping an apple is an act of everyday life, but the conclusion seemed almost a fantasy. Einstein’s thought experiment had discerned that there was no way for a person to distinguish if they are in a rocket controlled elevator, or under the influence of the gravity from a planet. At face value, the conclusions would seem to be this: since I can’t tell the difference between gravity and a rocket, maybe gravity isn’t real at all.

Any normal person might throw up their hands in exasperation and decide this discussion of the Equivalence Principle is nonsense and go work on something simpler (like brain neurochemistry). But Einstein was a persistent fellow, and pushed a little harder.  He asked, “Is this the real life? Is this just fantasy?” Could it really be the case that there is no way to tell if you are in a gravitational field? What can we experience — what can we observe — that convinces us that we are caught in the grip of gravity?

We understand the world through experiments; they are the medium by which we observe. All experiments — thought experiments in particular — are recipes. Experiments produce results (knowledge about the Cosmos) the same way a recipe produces a cookie. We look at that result, and we ask ourselves a few fundamental questions — they are the same for physics experiments as cookies. Why is the result this way? Can I change what went into the result? Will I get a different result if I change what I put in?

Science and baking are both built around experiments that seek to discover what small changes reveal about the world. In cookies, a relatively small change can change a chocolate cookie into an almost identical vanilla cookie (TOP). A more substantial but not completely different approach might make a peanut butter cookie (BOTTOM). But getting a chocolate chip cookie (RIGHT) takes a completely different approach. [Photo by S. Larson; I don’t know what happened to these cookies after the #science was done; sorry.]

Science is a game of tearing apart ideas and seeing what makes them tick. Changing the assumptions, the recipe of the experiment, could change the outcome. So once again, Einstein returned to our thought experiment with the elevators, and imagined something new. There is a big assumption hidden in our thought experiment — the rooms you and I were confined to were “small.”

Why should that matter? Let’s imagine that our rooms were larger — much larger — and consider each of them in turn.

First, think about your room, on a spaceship. This is a BIG spaceship, of the sort that only the Galactic Empire has the metal and economic resources to build. The entire bottom of the spaceship is covered by rockets, all of them pushing with the same force to make you go.  Now conduct the apple dropping experiment again, first at one end of the spaceship, and then at the other end, very far away.  Both apple drops show the same thing — the apple falls directly down, parallel to the walls of your spaceship.

No matter how large you make a room, if it is being propelled uniformly by rockets, apples all over the room fall straight to the floor, along paths that are everywhere parallel to one another.

Now think about my room, on the planet Earth. This is a BIG room, far larger than any room ever built as it is large enough that if my floors are flat, the curvature of the Earth falls away from under my room at both ends (though I am not aware of this — no windows, right?). If I drop my apple at either end of my huge room I make an astonishing discovery — my apple does not fall parallel to the wall! It lands farther from the wall than it started. Given the outcome of my experiment, I could imagine all sorts of plausible explanations.

Perhaps the walls of my gigantic room are repulsive.

Maybe the walls are repulsive!

That’s an interesting idea; maybe it’s true, maybe it’s not. Can I test it?

Sure!  I build a few new walls at different places in the big room and drop many apples many times. What I find is this: if a wall is closer to the center of the room, a dropped apple falls closer to straight down. At the exact center of the room, two apples fall straight down and land the same distance apart as when they were released. Two apples dropped at opposite ends of the room are closer together when they land on the floor! Physicists get grandiloquent about this and call it “tidal deviation.”

What is going on? The walls clearly aren’t repulsive — a wall in the center of the room doesn’t push apples away from it at all.  We have talked about the lines of force that show the gravitational field.  The gravitational field always points to the center of the source of gravity. What this experiment seems to show is that if my room is big enough, I can detect the shape of the gravitational field!

(TOP) When my apples are dropped, their paths are not parallel; we say there is a tidal deviation between the paths. This is a key experimental signature of gravity. (BOTTOM) We can understand the tidal deviation of the apple paths if we imagine they are following the lines of force in the gravitational field (this is how Newton would have explained it). But this is not the only way to explain gravity!

This idea of the shape of the gravitational field, and its relation to the motion of falling objects, would be a key part of Einstein’s mathematical development of general relativity: it led him to the thought that motion and geometry could be connected.

That may seem like an odd thought, but the fundamental building blocks of elementary geometry are exactly the elements of motion that we discovered in our Giant Room Apple Dropping Experiments: lines can be parallel or not parallel. Einstein recognized that was important, so he explored it. We can too! Let’s think about a flat table top.

If I have two Matchbox cars on my table, and give them a push, they travel in a straight line and never stop (in the absence of friction — every little kid’s dream!).  If I take those two cars and set them in motion  exactly parallel to one another, what happens? The two cars speed off across the table and their paths never cross, no matter how far they go. In many ways, this example is like our two apples on opposite ends of the Gigantic Rocket-Propelled Room — the apples both started falling on straight lines, parallel to each other, and they ended up hitting the floor falling on straight lines that were still parallel to each other.

On a flat surface, two lines that begin parallel stay parallel, no matter how far you extend the lines across the surface.

So this leads to the inevitable question: is there a way in geometry to make the Matchbox cars start out along parallel paths, but ultimately draw closer together? This would be analogous to the Gigantic Room the size of Earth, where apples dropped on opposite ends of the room landed closer together.  As it turns out, the answer to this question is YES.

Imagine a sphere, like a playground ball or a desk globe.  The surface of the globe is two dimensional, just like the table top — there are only two directions you can go: front-back, or left-right. Suppose I take my two cars and set them on the equator in different spots, but both are initially travelling due north — the paths are parallel! What happens? Eventually, the paths of the two cars get closer together, and if we wait long enough, they cross.

If two travellers start at the equator travelling due north, their paths are initially parallel. By the time they reach the top of the globe, their paths cross each other — the paths don’t remain parallel because of the curvature of the globe!

Now, that is no way for parallel lines to behave on a piece of flat two-dimensional paper, but it is perfectly acceptable on a two-dimensional curved surface. THIS is the watershed idea of general relativity — maybe we can describe gravity as curvature. Maybe we can replace the concept of a gravitational force with the idea of particles moving on a curved surface — on flat surfaces, motion along parallel paths stay parallel, but on curved surfaces initially parallel pathways can converge and cross.

Neat idea. But curvature of what?!

Different ways we have devised to measure space or time.

Einstein brilliantly deduced that since our concern is with the motion of things, it should be curvature of the quantities that we use to describe motion — space and time. Special relativity, which motivated our reconsideration of gravity, was wholly focused on how we measure space and time, and Einstein’s former professor, Hermann Minkowski, had discovered that individually space and time are artificial elements of a single medium — spacetime.  Spacetime is the fabric of the Cosmos, the medium on which all things move. Einstein had become well versed in this notion, and concluded:

Gravity is the curvature of spacetime.

This is the heart of general relativity. So how does it work? General relativity is summarized mathematically by 10 coupled, non-linear, partial differential equations known as the Einstein Field Equations, succinctly written as

Fortunately for us, this mathematics can be captured in a simple, two-line mantra to guide intuition:

Space tells matter how to move.

Matter tells space how to curve.

In geometric gravity — general relativity — you can imagine spacetime like a large, deformable sheet. A particle can move anywhere on that sheet, so long as it stays on the sheet.  In places where the sheet is flat (“flat space”) the particle moves in an absolutely straight line.

But what happens if a particle encounters a large depression on the sheet? The only rule is the particle has to stay in contact with the sheet. It continues to travel in the straightest line it can, but if its path dips down into the depression, the direction the particle is travelling is slightly altered, such that when it emerges on the far side, it is travelling in a new direction that is not parallel to its original course!  Space tells matter how to move, with its shape.

Far from sources of gravity (edges of the sheet) spacetime is flat, and objects travel on straight lines. Small masses warp spacetime into a gravitational well (left dimple), while larger masses make larger gravitational wells (right dimple). If a particle comes close to a gravitational well, the curvature of spacetime bends its pathway. If a particle gets trapped in a gravitational well, the curvature of spacetime forces it to travel on a closed pathway — an orbit.

How do you curve spacetime?  With matter. The large, deformable sheet of spacetime is dimpled wherever there is a large concentration of mass; the larger the mass, the larger the dimple. Matter tells space how to curve, with its mass.  The larger the dimple, the larger deflection a particle passing nearby will feel. This at last, is the long awaited connection to the way we think about Newtonian gravity — the source of gravity is always matter, as we expected.

So we have done away with the concept of a “gravitational force field” and replaced it with the idea of “motion on a curved spacetime.” An astute reader will ask a pertinent question: if general relativity is really the way gravity works, why didn’t we discover it first? Where did Newtonian gravity come from?

Both Newtonian gravity and general relativity make exactly the same predictions when gravity is weak and speeds are slow.  In fact, mathematically, general relativity looks just like Newtonian gravity at slow speeds and in weak gravity. These are precisely the conditions we encounter in the solar system, which is why Newtonian gravity was discovered first, instead of general relativity!

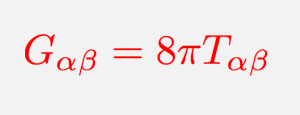
You may have encountered models of spacetime gravitational wells out in the world. This one, in the Milwaukee Airport, captures coins for a museum. [Photo by K. Breivik]

It’s fine, of course, to make up a new idea about gravity. But this is science — fancy theories are only as good as the tests that can be conducted to verify them.  Einstein knew this, and proposed a series of tests for general relativity, which we’ll talk about next time.

PS: I rather enjoyed using Bohemian Rhapsody to start this bit of the General Relativity story. It was written by the great Freddie Mercury for Queen’s 1975 album, “A Night at the Opera.” As we shall see in our next installment, Mercury (the planet) plays an important role in bringing the importance of General Relativity to the attention of the scientific community, just like Mercury (Freddie) helped me explain it here. 🙂

PPS: This week I couldn’t capture all of this in one 3 minute video, so I tried to do it in two.

—————————————

This post is part of an ongoing series written for the General Relativity Centennial, celebrating 100 years of gravity (1915-2015).  You can find the first post in the series, with links to the successive posts in this series here: http://wp.me/p19G0g-ru.

Gravity 1: Seeing the Invisible

by Shane L. Larson

General Relativity is only the latest refinement of our ever growing understanding of gravity. Most of us become aware of gravity at a very young age. It is a playmate when we throw balls, an accomplice when we knock our unwanted food off the table, and our Nemesis as we learn to stand up and walk. All things being equal, gravity is a source of much mayhem when we are children, but hidden in the chaos we learn a few things, and we learn them deeply. When we drop things, they fall. When we jump in the air, we always come back down. It is such a pervasive part of our lives, that we seldom give it a second thought. Once you start school, you learn that gravity is a thing, and that thing keeps you on the floor, makes rain fall from the sky, and makes planets go around the Sun.  Gravity is something you learn about in science class. But why is it a part of science class, when you learned about it as a toddler?

(TOP) Most of us develop an intimate relationship with gravity at a very young age. (BOTTOM) Whether we know it or not, gravity impacts all aspects of our every day life in subtle ways.

The job of a scientist (and a toddler) is to look at the world around us, take note of those “obvious” things that we don’t even give a second thought to, and ask “why is the world that way?” The answers to that question enable us to harness Nature by predicting the future. If I understand gravity, I can figure out how strong a building needs to be without tipping over (like the Leaning Tower of Pisa), I can figure out how much pressure a water tower will provide for a city, or I can figure out how big to make an airplane wing so it can fly.  There is other physics to be sure in all of these, but gravity is at the heart of it all, just as we learned as children.

The authors of our fundamental thinking about gravity. (L) Isaac Newton, who developed the Universal Law of Gravitation and (R) Albert Einstein, who developed General Relativity.

So how do we think about gravity? After all, it is not like an orange or a Lego brick — it’s not something tangible that you can pick up. In fact, if anything, it is totally invisible! The discovery of the invisible and how to talk about it is still one of the greatest feats of the human imagination. The first person to do this for gravity, was Isaac Newton. Fundamentally, Newton put us on the path to describing gravity using mathematics, the language of science. He first wrote down the Universal Law of Gravitation in his 1687  book, the Principia, along with all the math you needed to work with the Universal Law (read: calculus). Einstein refined and extended our understanding of gravity by writing down general relativity using a new mathematical approach: curvature and tensor calculus.

But learning how gravity works in the Cosmos from mathematics can take years of practice and patient study. Fortunately, we can develop some intuition about how gravity works by learning to draw some simple pictures.

Physicists describe the long range effect of gravity using the concept of a “force field,” or simply a “field.” As is often the case with spoken language, scientists adopt common words to mean very specific things that don’t always jive with what the rest of us think the word means. What do you think of when I say “field?” If you’re a country kid like me, you may imagine a vast expanse of rolling hillsides in eastern Oregon, stalks of wheat heavy with ripening grain rippling as the wind blows across the “field.” Others of you may imagine a late July afternoon, the hot sun shining down on the bleachers in Wrigley Field as the Cubs once again try to chalk up a win in the run to the pennant. Neither of these examples is what a scientist means by “field,” but they both have an important element to the scientific definition — big, open spaces.

Some other kinds of fields.

An important part of understanding gravity is recognizing that no matter where you are in space, if there is a source of gravity somewhere (say a planet, or a star), then you feel the tug of that gravity. Gravity fills all of space. That simple fact leads to the concept of a “field” in physics. We are going to draw pictures of fields, but there is a robust and well understood mathematical treatment of fields that will give you the same intuition (and more) as our simple pictorial model.

So how do we draw a picture of the “gravitational field?” The rules are:

• Draw arrows to represent the “gravitational force.” Those arrows fill all of space, and point toward the source of gravity (the direction that gravity is trying to pull you); they are usually called “lines of force.”
• Big, massive objects have more gravity than small objects, so they have more arrows pointing toward them — they exert more gravitational force on their surroundings.
• The gravity any object experiences is understood by how closely packed the field lines are in the vicinity. Lots of field lines near you equates with stronger gravity in your vicinity.

Demonstration of the drawing of gravitational “fields.” [TOP] The field lines (lines of force) point toward the mass creating the gravity. The number of field lines depends on the mass of the object; more mass, more field lines. [BOTTOM] What you feel in terms of gravitational forces depends on how many field lines are around you. The gravitational force felt far away from the source of gravity is weaker, evidenced in our picture view by fewer field lines.

So how do we use this pictorial approach to gravity in practice? Let’s imagine a trip to one of the most picturesque destinations in our solar system: Jupiter. Spacecraft from Earth have visited Jupiter nine times so far.  They have returned stunning pictures and made astonishing discoveries about Jupiter and it’s ragtag group of moons.

The planet itself is enormous, comprised mostly of gas surrounding a small rocky core. Deep beneath the clouds the pressure and temperature soar, making Jupiter glow in the infrared, cloaked in the light of its own inner heat.

On the top of the clouds, an enormous cyclonic storm has roiled and churned for at least the last 400 years, sometimes growing to three times the size of the Earth. We call it “The Great Red Spot.”

Among Jupiter’s entourage of moons is a wild and unpredictable world with volcanoes that spew molten sulfur 500 kilometers into space. This is the most volcanically active world we know, called Io.

In 1992, Comet Shoemaker-Levy 9 strayed too close to Jupiter and was torn apart into 22 fragments. In 1994, as we watched from the relative safety of Earth, each of those 22 chunks of rock and ice pummeled into Jupiter one after another.  Any one of them could have leveled our cuvilization; they burned and scarred the clouds of Jupiter, but over time even those marks faded into memory and Jupiter kept on about its business as if nothing had happened.

Wonders of the Jupiter system, all ultimately connected to Jupiter’s strong gravity. (L to R) Jupiter glows in the infrared; the 400+ year old storm known as the Great Red Spot; the volcanic moon Io; the scars left by the impact of Comet Shoemaker-Levy 9, crushed by Jupiter’s gravity.

Each of these wonders, each of these  strange and wonderful things we have discovered at Jupiter, are a consequence of Jupiter’s enormous gravity.

Let’s draw the picture of Jupiter’s gravitational field. The number of field lines is related to the mass of the planet. Suppose we drew 10 lines to represent the gravity of the Earth. Jupiter is 318 times more massive than Earth, so we should draw 3180 lines to represent the gravitational field of Jupiter!  That’s too many to easily see, so let’s just think about Jupiter’s own gravity, and decide it can be represented by 8 lines.

The gravitational field fills all of space, so no matter where you are, you feel the tug of Jupiter pulling on you, from wherever you are, directly toward Jupiter. Far from the planet, the lines are more widely spaced, so gravity is weaker than it is down close to the planet where the lines are closer together.

Rodin’s “The Thinker” is probably engaged in a gedanken experiment.

Now, let’s conduct a gedanken experiment — a thought experiment — together. This is a time honored method in theoretical physics to try and understand how the world works. The basic idea is this:

(0) Suppose you have some aspect of Nature you are trying to understand; in this case, the “field description” of gravity.

(1) Imagine a situation to which the law of physics should apply. This could be a situation that could legitimately be addressed in the laboratory with an experiment, given enough time and money, or it could be a physical situation that we can’t recreate but might encounter in Nature. This second case is the one we would like to consider, as it involves the gravitational field of an entire planet.

(2) Apply the law of physics to your situation, and examine all the possible outcomes that would result if you could actually do the experiment for real.

(3) Lastly, you examine the consequences of your gedanken experiment by asking legitimate questions and answering them. Do the predicted outcomes make sense? Do any of the outcomes violate the laws of physics? Are there observational consequences that we might be able to see that would confirm our gedanken experiment?

For our thought experiment, let’s imagine we had the ability to simply squeeze Jupiter and make it smaller. We don’t want to take any mass away, or add any mass to it, we simply want to squeeze it into a smaller, denser ball of stuff, and ask what happens to the gravitational field.

If we follow our rules for drawing fields: (1) The number of field lines won’t change, because the mass of Jupiter doesn’t change. (2) The field lines fill all of space. When we squeeze Jupiter smaller, the field lines in the picture already fill space far away from Jupiter, so we just need to extend down toward the new, smaller Jupiter.

(L) Jupiter’s gravitational field is stronger near the surface, and weaker far away. (R) If I shrink Jupiter without changing its mass, the field stays the same far away, but it gets stronger at the surface!

Now we examine the consequences of our experiment. Far away from Jupiter, nothing has changed. The same number and spacing of field lines are present with the big or the small Jupiter. If you’re an astronaut, drifting aimlessly in orbit around Jupiter, nothing noticeable happens.  But in close, things are a bit different. In the case of the big Jupiter, if we hovered over the clouds we felt some pretty strong gravity. If we compare that to the case of hovering over the clouds of the new small Jupiter, we feel even stronger gravity! How do we know this? Because near the new small Jupiter, the field lines are closer together.

So what do we conclude from this? The “surface gravity” of an astronomical body depends on the compactness (or, more properly, the density) of the planet/star/thing in question. Far away from the astronomical body, the gravitational field depends only on the total mass of the object.

Can we observe these effects for real, somewhere in the Cosmos? Yes!

White dwarfs are the size of the Earth, but the mass of the Sun. The result is a huge gravity at the surface!

When a star like the Sun reaches the end of its life, it does not explode. Instead, it shrinks to a husk of its former self, a shriveled skeleton known as a white dwarf.  White dwarfs are about the size of Earth, but have the same mass as the Sun. We observe atoms moving in their atmospheres, just over the surface and find that the surface gravity is a staggering 10,000 times greater than the surface gravity of the Sun. By a similar token, many white dwarfs orbit companion stars, and some have been observed to have planets (perhaps long ago, and we just didn’t realize it), all of which are far from the white dwarf but careen happily along their orbits as if they were orbiting an ordinary, Sun-like star.

These observations agree handily with our gedanken experiment.  We used our pictorial model to deduce that if you squeeze an object smaller without changing its mass, the surface gravity changes, but the gravity far away does not!

The Cosmos, and our brains, have not let us down. We’ll put these ideas to the test again, as we delve into the development of General Relativity and encounter even stranger and denser objects — black holes.

—————————————

This post is part of an ongoing series written for the General Relativity Centennial, celebrating 100 years of gravity (1915-2015).  You can find the first post in the series, with links to the successive posts in this series here: http://wp.me/p19G0g-ru

Gravity 0: Discovering Gravity

by Shane L. Larson

You and I live in the future. We are connected to each other in ways that would have stunned people who lived only a century ago. I had the good fortune growing up to know my great-grandmother, who lived to be 98 years old. My Grandma Dora was born in 1895, at a time before electricity and telephones and automobiles were commonplace. The mode of transportation when she was born was the horse and buggy, though steam had been harnessed and train lines were beginning to gird the world. The Wright Flyer would not make its first epic flight at Kitty Hawk until 1903, when Grandma Dora was 8 years old. But she lived to see humans sail the void of space, space shuttles ply the skies, and humans walk on the Moon. In just about 100 years, the span of a single human life, she saw the world change.

(L) My great-grandmother Dora [center] with her sisters Mary [left] and Arta [right] in the early 1900s. (R) Around this same time, the Wright Brothers made their historic flight at Kitty Hawk, in 1903.

When she was just a girl, there was a young man living halfway around the world, in Bern, Switzerland. The Industrial Revolution was in full swing, and creative minds the world over were trying to imagine how to use technology and machines to change our lives, and how to patent those ideas and make money. Some of those attempts to capitalize on the rapidly evolving world wound their way through the Bern Patent Office (the Swiss Federal Institute of Intellectual Property) to the desk of Albert Einstein. For the young Einstein, a trained technical professional, the job at the patent office was just that — a job. He very much wanted to be a professor and work on science, so in the evenings he committed himself to physics the way some of us work day jobs but in the evenings work on writing novels (or blog posts about science). In 1905, those evening endeavours paid off when Einstein published four seminal papers that transformed his life, physics, and the world forever.

(L) Einstein when he was working at the Patent Office in Bern. (R) Einstein’s living room, still preserved, in the first floor apartment where he worked on special relativity during his years at the Patent Office.

Among those papers was the original paper to describe special relativity — the laws that govern physics at high speeds, approaching the speed of light. Nestled in that paper is one of the most important discoveries in physics and the one most germane to our story here:

Nothing can travel faster than the speed of light.

This was a stunning realization, because up to that point no one had ever really imagined that we couldn’t go faster than light. The speed of light had been measured famously by Danish astronomer Ole Romer in 1676 and by French physicist Hippolyte Louis Fizeau in 1849. But there had never been a reason to believe that the speed of light was the ultimate speed limit in the Cosmos.

Folklore is that Newton witnessed the falling of an apple when visiting his mother’s farm, inspiring him to think about gravity. It almost certain is apocryphal that it hit him on the head, but this was the beginning of the Universal Law of Gravitation, one of the most successful descriptions of Nature ever invented.

With Einstein’s realization, we began to examine the laws of physics that had been discovered up to that point, and we found a curious fact. Some of those laws, unbeknownst to us, had the secret about light hiding in them, like a pearl in an oyster.  Most notable among these were Maxwell’s Equations for Electrodynamics. Curiously, Newtonian Gravity did not have the ultimate speed limit. The classical Universal Law of Gravitation, which Newton had penned more than 200 years earlier, was built on the idea of instantaneous communication over any distance, an impossibility if there was a maximum speed of travel. Einstein recognized this and set about to resolve the issue. He would dedicate the next 10 years of his life to the endeavour. During those years, he would finally leave his job at the patent office for the life of an academic, holding professor positions at several universities around Europe. All the while, he worked steadfastly on merging gravity and special relativity.

This was not a simple matter of “imagining something new.” Newtonian gravity worked perfectly well in the solar system, where things moved slowly and gravity was weak. Einstein knew that whatever Nature was doing with gravity, it had to look like Newtonian Universal Gravity at slow speeds and in weak gravity, but not be confined by instantaneous propagation of signals. He went through a meticulous procession of thought experiments, explored new applications of mathematics (the language of science) and developed new intuitive ways of thinking about gravity. His long hours and years of brain-bending culminated in 1915 with his presentation of the Field Equations of General Relativity, now known as the Einstein Field Equations.

In 1902, Georges Méliès (L) created the film “Le Voyage Dans La Lune” where an enormous cannon (C) was used to launch a space capsule carrying explorers to the Moon (R).

I think about this age of the world often, my thoughts fueled by memories of talking with my great-grandmother. What was the world like when the young Einstein was thinking about lightspeed and gravity?  It was an age of horse and buggy travel. What was the fastest people could imagine travelling in that era? In 1903 the great French director Georges Méliès told at tale of travelling to the Moon — “Le Voyage dans la Lune” — using a new technology called “moving pictures.” In that remarkable tale, he imagined a band of intrepid explorers attaining great speeds by being launched from an enormous cannon, still far slower than the speed of light.

The horse and buggy set the speed of life in those days. This is an ambulance for the Bellevue Hospital in New York in 1895, the year my grandmother was born.

The speed of life was slow in those days, far slower than the speed that Einstein was contemplating.  But still Einstein was able to apply his intellect to a question that perhaps seemed outrageous or unwarranted. At the time, the derivation of general relativity was mostly a curiosity, but today, a century later, it plays a central role in astrophysics, cosmology, and as it turns out, in your everyday lives!

Applications of general relativity, and the frontiers of general relativity in modern physics and astronomy. (TL) GPS system. (TR) Planetary orbits (LL) Black holes (LC) Wormholes (LR) Singularities.

In 2015 we are celebrating the Centennial of General Relativity. That means all your gravitational physicist friends will be all a-pitter-patter with excitement for the next 12 months, and impossible to quiet down about gravity at dinner parties.

On the off chance that you don’t have any gravitational physics friends (gasp!), for the next 13 weeks I’ll be exploring the landscape of general relativity right here at this blog. We’ll talk about how we think about gravity, the history of testing and understanding general relativity, modern observatories that are looking at the Universe with gravity instead of light, and some of the extreme predictions of general relativity — wormholes, black holes, and singularities.

My great-grandmother, Dora Larson.

My great grandmother passed away shortly after I went to graduate school, where I made gravity and general relativity my profession. In a time shorter than the span of her life, this little corner of physics had grown from the mind of a patent clerk into one of the most important aspects of modern astrophysics, at the frontiers of scientific research. Grandma Dora and I never got the chance to sit around and talk about black holes or the equivalence principle, but I often wonder what she would have thought of all the hoopla that gravity commands in modern life and modern science? What would she have seen, through eyes that saw the world grow up from horse drawn carts to space shuttles and GPS satellites?

—————————————

This post is part of an ongoing series written for the General Relativity Centennial, celebrating 100 years of gravity (1915-2015).  This is the introductory post of the series. For the first time, I’m trying short 3.5 min videos with each post to capture the essential bits of each one. Here is the YouTube Playlist with all the videos (let me know how you like them — it’s an experiment!).

Links to the successive blog posts in this series are below for reference:

Gravity 0: Discovering Gravity (28 Dec 2014)

Gravity 1: Seeing the Invisible (7 Jan 2014)

Gravity 2: The Road to General Relativity (15 Jan 2015)

Gravity 3: Curvature & the Landscape of the Cosmos (24 Jan 2015)

Gravity 4: Testing the New Gravity (7 Feb 2015)

Gravity 5: Putting Einstein in the Navigator’s Seat (12 Feb 2015)

Gravity 6: Black Holes (28 Feb 2015)

Gravity 7: Recipe for Destruction (Making Black Holes) (7 Mar 2015)

Gravity 8: Black Holes in the Cosmos (15 Mar 2015)

Gravity 9: The Evolving Universe (27 March 2015)

Gravity 10: Signatures of the Big Bang (8 April 2015)

Gravity 11: Ripples in Spacetime (24 April 2015)

Gravity 12: Listening for the Whispers of Gravity (14 May 2015)

Gravity 13: Frontiers (27 May 2015)