The Hardest Thing About Science I: Language

by Shane L. Larson

One of the “features” of the modern world is memes percolating through our social media feeds, online browsing, and texts from friends. Sometimes these memes are humorous images, sometimes they are captures of tweets and posts, sometimes they are interesting facts. Let’s spend a few moments considering these last ones.

Examples of common memes that relay information or observations about science [Images via your favorite local internet browser].

Memes that relay “interesting facts” are often tidbits of history, trivia, or scientific knowledge that are surprising or provocative. Many of these memes are absolutely correct, yet surprising, and they get rebroadcast over and over again.

Why are such memes surprising and appealing? Sometimes they remind us of how little we know, or how it used to be when we were in school, or how silly complex questions can sound. They play with our deeply rooted notions of humor, playing word or pun games that juxtapose everyday language against the language of science. Chemistry memes are particularly good at this, where designations for the chemical elements — the 92 naturally occurring substances that the Universe creates everything from — are used to create words or funny turns of phrase. Like this meme about the element mercury, represented by its chemical symbol “Hg” (which comes from the Latin word for mercury, hydrargyrum — literally “liquid silver”).

Sometimes the reason is the propositions of science are used as beacons of stability in a world rife with randomness and illogic. Particularly in today’s world, where ideological arguments boiled down to soundbites are casually tossed around without much thought, people long for the ideals of impassioned debate moderated by reason and data. This is of course the standard that science aspires to, so memes promoting such ideals are popular.

But the memes of considerable interest are the ones that give you pause, and provide a delectable moment of cognitive dissonance. They challenge your thinking and world-view about something that seems ordinary, but apparently is not. 

Consider this very common repeated science factoid about the color magenta.

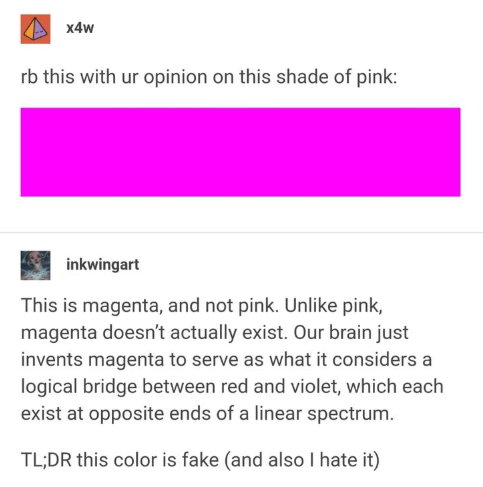
If you are like most people, you may read this and go, “What? WTF does this mean? Of course magenta exists! Look at this shade of lipstick right here!”

But to understand what is going on here, we have to dissect every little bit of the meme. First, of course “magenta” exists, because that square of color is clearly there, and recognizable in the array of colors people might call “magenta.” But the second part is the piece to consider carefully: it is a color your brain is using to interpolate between red and violet. This is where the science part of this factoid is. It has been presented to drive you into cognitive dissonance, but no effort has been made to really help you understand what it means in the concrete world of science… this is the failure of such memes.

It does, however, illustrate one of the hardest things about science: the imprecision of language. Human language, which we depend on every single day and use as a malleable all-purpose tool, cannot easily convey with precision and accuracy what science has to say about most phenomena in the world. Color is a classic example. What does a scientist mean if they make a pithy statement like “magenta does not exist”? They mean something very precise, but the language of our common vernacular means something quite different.

Consider the color in this image. What color do you name this? Show it around to family and friends and ask them what color they call it. You will get a wide range of answers: green, yellow-green, fluorescent green, fluorescent yellow, fire-engine green, safety-vest yellow. Well, what color is it? We all recognize this color, but there is no universal name for it, though using any of these names mentioned, and a few examples, would quickly firm up the color under discussion in conversation.

But that isn’t precise enough or good enough for science. Scientists need to know exactly what color is under discussion — perhaps they are trying to create an LED light to create that color, or making a sensor that responds only to that particular color when it is scanned. In this case, this color is very close to the dominant color of light shed by our parent star, the Sun — the reason we use this color for attention and safety is your eye has evolved over millions of years to be sensitive to this color.

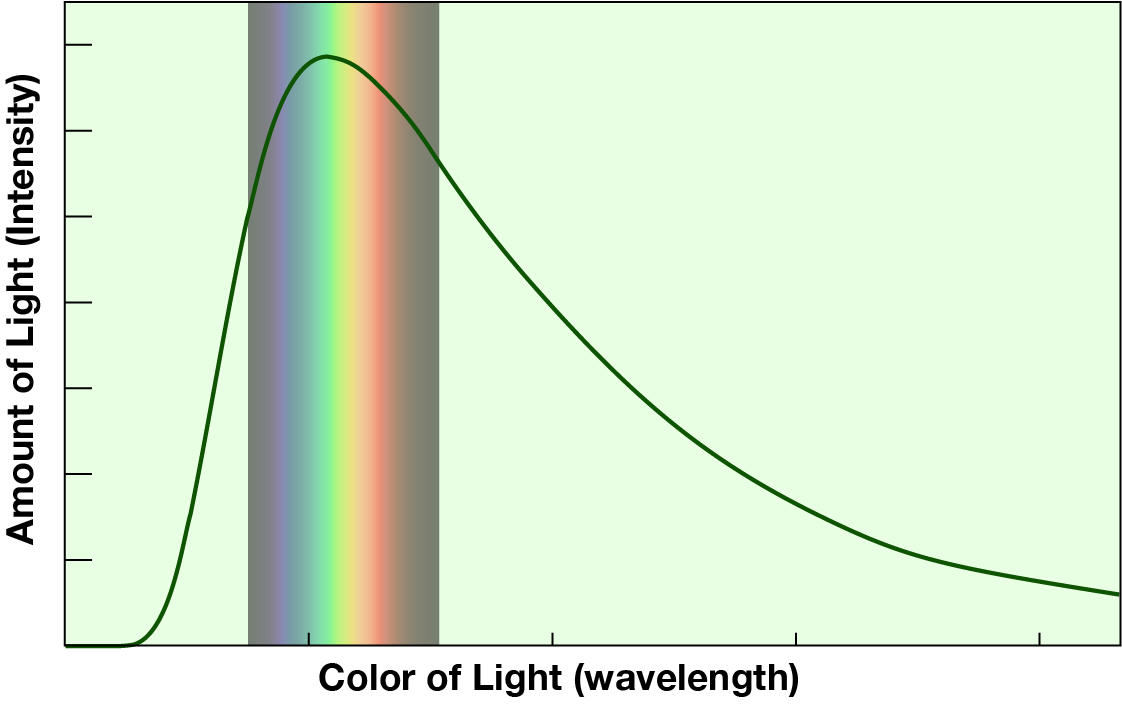
The “blackbody spectrum” of the Sun. The hill-shaped curve shows how much light the Sun emits in each color, and it peaks in the “safety-vest yellow” range of colors (at a wavelength of 500 nanometers). [Image: S. Larson]

So what do scientists do, when language isn’t up to the task? We layer on a bit of mathematics. In the case of color, physicists use a number called wavelength (often denoted by a lower case Greek letter lambda: λ). In the classic rainbow spectrum of light, cast by raindrops or sun-catcher prisms, or bevels on your windows, every single color has a unique number that scientists use to identify it.

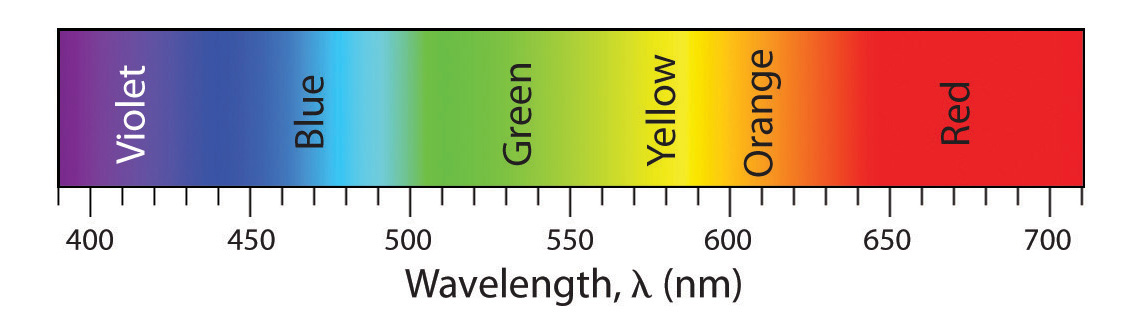
The approximate colors and associated wavelengths of light that are visible to the human eye (the “visible spectrum”). [Image: S. Larson]

In the communication of scientific ideas, this ability to clearly and unambiguously quantify something is critical. Consider the following two conversations about color:

Conversation 1:

    Father: I put your red jacket in the closet.
    Daughter: I don’t have a red jacket.
    Father: Yes you do, you wear it every day.
    Daughter: Pop! That is burgundy.
    Father: <blank stare>

Conversation 2:

    Astronomer 1: It was too red to show in the image.
    Astronomer 2: The camera should have picked it up. 
    Astronomer 1: The wavelength was around 720 nanometers.
    Astronomer 2: Oh, you mean really red.

As astronomers, we still depend on language just like everyone else, but we have a mechanism to fall back on more precise statements and specifications needed to understand the world around us. In the case of color, that is wavelength.

But what about the magenta? What does it mean that it “doesn’t exist”? It means that for a scientist, there is no quantifiable number — no wavelength — that identifies where in the spectrum of light the color you and I call “magenta” can be found. It cannot be found in the spectrum! Yet it clearly exists when you and I stare at this little colored square. It is, in fact, a mixture of pure colors from the spectrum — the violet and the red mentioned in the original meme.

In the rainbow spectrum, where each color has its own unique numeric label, if you take a bit the violet color, and mix it with a bit of the red color, and throw that light at your eye, your brain says “whoa! look at that magenta!” 

In many ways, the meme is being dishonest to get a shock out of you. The amount of violet and red to be mixed can be quantified to make different shades of magenta — otherwise printers and lipstick makers would have a much rougher time making things this color! There is an exact, quantifiable way to specify every shade of magenta you put on the table. 

Nature can make magenta, but Nature doesn’t make magenta as a fundamental building block.

Salt crystals are not fundamental objects; salt itself is a combination of fundamental elements, sodium and chlorine. [Image: Wikimedia Commons]

It’s no different than elemental chemistry. “Salt” does not exist on the periodic table, but salt clearly exists in the same way magenta exists. In the fundamental, quantifiable world of the chemical elements (the building blocks of which everything on Earth is made), there are two uniquely identified substances: one is called sodium (Na) and one is called chlorine (Cl), and when I bond them together, I get something that is not elemental, but a mixture that we call NaCl — sodium chloride, or “salt.”

Saying something “doesn’t exist” has a multitude of interpretational meanings, but it means something very specific and very precise.  In the context we’ve been discussing here it doesn’t mean you can’t find something you and I would call “magenta” in the Cosmos — it means none of the fundamental building blocks of color, the rainbow of light, are called “magenta.”

This is one of the hardest things about science. Language is evocative and emotional and nuanced and, ultimately, imprecise. And since we are social creatures who in large part think in terms of language and act in response to language, it makes it hard — very hard! — for our brains to engage in the discovery of the world around us with the rational, quantifiable approach of science.

Moreover, it is hard to express personal enthusiasm and joy for the wisdom and knowledge that science has brought our species, when science itself is ideally more grounded — that dichotomy make the communication of science using this ratty tool we call “language” all the more difficult.

But we still try. With a few funny graphics and memes, a few stories and quips, and a few written words like these ones here…

——————————————————-

This post is the first in a short series pondering what kinds of things make science difficult. The posts in this series are:

1: The Hardest Thing About Science – Language (this post)

2: The Hardest Thing About Science – Nouns & Verbs

The Commonality of Armageddon, Oreos, & Shakespeare’s “A Midsummer Night’s Dream”

by Shane L. Larson

I love internet memes because they capture the awesome absurdity of modern life. While not unique, I am apparently a member of a small minority among scientists — I can see some commentary on modern life (such as an internet meme) or watch a Hollywood spectacle (like Armageddon) completely detached from the scientific processors in my brain, and enjoy the rush of brain chemicals that make me happy and content.  The ability to “suspend disbelief” and live in the moment is hard for many scientists.

Why is that? As scientists, we are trained to exercise our detached personas in an attempt to view the world as an independent and unbiased observer. This is, of course, completely contrary to human nature — scientists always bring our personal prejudices to the table, and view Nature through the lens of our own biases.  We are human, after all.  But the mechanism of science is designed to protect us.  Experiments can be and should be repeated.  The outcomes of observations are examined and questioned from every viewpoint, looking for inconsistencies.  When inconsistencies are found, new experiments are done or new ideas are proposed and then reexamined.  The entire process is repeated over and over and over; it never ends.  Changing your mind in the face of new data and new ideas is encouraged, and widely accepted as “best practices.”  If you don’t “flip-flop” in science, then you aren’t doing it right. If you cling to old ideas in the face of contrary and overwhelming experimental evidence, then you aren’t doing it right. Science is designed to be a self-correcting process, so that the more experiments and observations that are completed, the less likely that our understanding of Nature is wrong.

What does that mean, “less likely?”  What does a “low probability” or a “high probability” mean, and how do we figure such things out?  Let’s revisit one of my favorite internet memes to understand this.  It has often been said that a million monkeys typing on a million typewriters will eventually create the entire works of William Shakespeare.

The beauty of science is it has very few boundaries. There are well prescribed methods to think about any question that is of interest or importance, like the idea of monkeys typing Shakespeare (an interesting intellectual exercise, though plausibly only important if you are afraid of a future like Planet of the Apes — http://en.wikipedia.org/wiki/Planet_of_the_Apes_(1968_film) ).

Let’s talk about “odds.” The odds of something occurring is the likelihood that some event may or may not happen. It is a much abused notion, and often used in weird ways, but we can understand the basic premise and think about our Internet meme with what we learn.

Let’s start with a simple example: flipping a Heads or Tails Oreo (chocolate Oreo on one side, Golden Oreo on the other; http://www.youtube.com/watch?v=YIS2dzNA6_E).  Our game will be this: if the Oreo comes up Golden, you get it. If it comes up Chocolate, I get it.  We each have a vested interest in the outcome of this experiment!  Now assuming you and I are both honest Oreo competitors, when we flip the Oreo there is no way to make one side come up more often than the other. If this is true, we call it a “fair Oreo” (if you are talking about coins or dice, this would be called a “fair coin” or “fair dice”).

So if I flip the Oreo, there is a “50-50 chance” you’ll get the cookie. What does that mean?  It means that your outcome (golden) is one (1) outcome out of two (2) possible outcomes (golden or chocolate):

number of desired outcomes/possible outcomes = 1/2 = 0.5 ➙ 50%

The way a math-nerd might explain this is if we take a thousand bags of Oreos, with 100 cookies in each bag, and flip them all, then on average, each of us will end up with 50 cookies from a bag.  That “on average” is an important statement — it hides a deep history of confusion, argument, discovery and understanding in mathematics. Statistics are not perfect; strange things do happen “against all odds” — that’s why they are called “odd occurrences!”

Now, let’s ask a more complicated question.  Suppose you and I are competing for TWO cookies.  What are the chances that one of us will end up with BOTH cookies, and the other one of us will cry?  I think about this in terms of a table like the one below.  How many ways can we get a golden Oreo?  Two: gold on the first toss (G1) or gold on the second toss (G2).  Similarly there are two ways to get a chocolate Oreo: chocolate on the first toss (C1) or chocolate on the second toss (C2).

The four possible outcomes of tossing two Oreos. This is often called a “probability table.”

These are all the possible outcomes of our friendly competition.  There are 4 ways this could go down — you could take all the cookies (G1-G2), I could take all the cookies (C1-C2), and there are two ways we could split the cookies and still be friends (C1-G2 and G1-C2).

Looking at the table, there is a 1 in 4 (1/4 = 0.25 ➙ 25%) chance you are the Cookie Monster ( http://www.youtube.com/watch?v=-eZ22B-2F5M ) and take both cookies.  Can I figure that out without making my table?  Sure!  In probability the chances of independent events happening is found by multiplying the chances of each event happening.  We said before there was a 1 in 2 (1/2 = 0.5 ➙ 50%) chance of the cookie coming up golden on any throw.  So if I make two tosses, then I get

Crazy!  Just so we’re clear here: if I won both cookies, I’d still give you one.  🙂

Now, let’s think about our monkeys, and Shakespeare.  After much googling, I can’t find anyone who knows how many letters there are in any given Shakespeare play. I am a big enough nerd to write a computer program to count the words in A Midsummer Night’s Dream, but I’d never admit to it in public — I have a reputation to uphold!  So let’s think about a simpler example.

What are the chances of a monkey randomly typing a single word at the computer keyboard, like “cookie.”  Let’s assume we have a simple keyboard with 27 keys — 26 letters and a spacebar.  The chance of our monkey hitting any particular key is 1 in 27 (1/27 = 0.037 ➙ 3.7%).  The chances of hitting the “c” followed by the “o” is then:

That’s not a very big number!  To get all six letters in “cookie” the odds are

We would usually say “there is about a 1 in 400 million chance of a monkey randomly typing the word cookie.”  Wow!  The value for a Shakespeare play would be even smaller — there are a lot of words to get right in a play.

But the internet is full of monkeys (as a survey of the comments on any blog will convince you).  With a lot of monkeys typing, one of them will surely type out Shakespeare!  Let’s look at that idea.  A Midsummer Night’s Dream is 2165 lines long.  Making a quick survey of the play, let’s assume there are about 45 characters per line, or 2165 x 45 = 97,425 characters our monkeys would have to get right.

First: what are the chances of one monkey getting it right?  Following our example of typing “cookie”, it should be 97,425 copies of (1/27) multiplied together.  That would be 1 divided by 97,425 copies of 27 multiplied together (in mathematical notation we would write 1/27^97,425). If you multiply 27 by itself 97,425 times, that is not just a HUGE number, it is mind-boggling large, so 1/27^97,425 is similarly mind-bogglingly small!  In science, we have a way of writing large and small numbers in a compact way, called scientific notation.  The basic idea is to write a number followed by a multiplicative factor of 10.

For example: 1 x 10³ means take the number 1, and multiply it by 10 three times.  Using the rule of multiplying by 10 that you learned in grade school (each time you multiply by 10, add a zero) this would be: 1 x 10³ = 1000.  Similarly, 7×10⁴ would be 7x10x10x10x10 = 70,000.

Now let’s use this to talk about our typing monkey.  We need to express 27^97,425.  In scientific notation, this is about 1 x 10^139,450 — a 1 followed by 139,450 zeroes.  The chances of one monkey typing out A Midsummer Night’s Dream is about 1/10^139,450.  To put it another way, we would need 10^139,450 monkeys typing before one of them would accidentally type A Midsummer Night’s Dream.

Is this a large number of monkeys?  It is a stupefyingly large number of monkeys — a number so large as to be meaningless in the context of the known Universe.  Consider: there are about 7 x 10²³ atoms in an Oreo cookie.  By contrast, there are about 1 x 10⁵⁷ atoms in the Sun.  The entire Milky Way galaxy harbors only 1 x 10⁶⁹ atoms, and there are only 1 x 10⁸⁰ atoms in the visible Universe.  To get one monkey to accidentally type a Shakespearean play, you would need more monkeys than there are atoms in the known Universe.  Since monkeys are made of more than one atom each, this seems unlikely.  🙂

Exercises like this are interesting diversions, but do they matter “in the real world?”  Of course; statistics rule our lives.  The ideas we have just used to talk about our Oreo Duel or typing monkeys are exactly the ideas needed to estimate your chances of surviving cancer, exactly the ideas need to estimate the number of cell phones a wireless network has to be able to support, and exactly the ideas needed to estimate the reliability of an unproven sky-crane to land a rover on Mars (http://mars.jpl.nasa.gov/).

The idea of monkeys randomly typing Shakespeare is an idiom of modern culture, never intended to accurately capture or express scientific understanding. Instead it captures a very human side of our psyche — the deeply ingrained notion that the world is random, that perhaps we don’t have as much control over the Cosmos as we would like.  But nothing could be further from the truth — art and science are the most beautiful testimonies one could imagine against the idea that our destinies are not ours to control.  Shakespeare was a genius without peer and created stories and tales of the human condition that have moved and inspired us, persisting long past his time.  Similarly, science is the manifestation of a long heritage of geniuses who have wrested from Nature the subtle rules and patterns that govern our seemingly random existence.  We can figure things out, and with that knowledge, improve our lives. We can write what we figure out down, to inspire our descendants and help them understand the world in which they live.

I am quite secure in my confidence that there is no problem that we cannot understand through the lens of science. It is comforting and awe-inspiring to me that we can figure things out.  Does that mean every problem is easy?  No. Our grasp on the engineering to travel to the stars is probably still very far away; comprehending the nature of the aging process  among animals (and how it is different when compared to plants, for instance) is probably still far away; understanding the nature of cancer is probably still far away.  But I’m confident that given enough time, enough resources, and enough applied brain power, any of these problems and a million others just like them could be resolved.  And you should be too.  So tuck that factoid in the back of your mind, and go watch Armageddon again — it’s escapist fantasy, but the kernel of truth is there: science has always got your back.