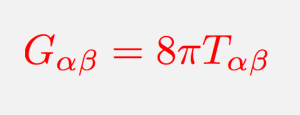Gravity 03: Curvature & the Landscape of the Cosmos

by Shane L. Larson

Had he been alive when Queen formed in 1970, perhaps Einstein might have jammed with them.

“Is this the real life? Is this just fantasy?”  So opens the classic rock song by Queen, Bohemian Rhapsody. Trying to understand modern gravity often puts one in the frame of mind that the mental machinations we go through are somehow not connected to reality. Albert Einstein’s genius was that he persevered through those uncomfortable feelings. He willfully ignored traditional ways of thinking about the real world, and imagined new and inventive ways to describe how Nature behaves.

One of those inventive ways of thinking was to noodle about unusual situations, like the Equivalence Principle. What a happy little thought — an idle daydream to imagine an elevator on the Earth, or flying in a rocket, and asking what would happen if you did something as simple as drop an apple? Dropping an apple is an act of everyday life, but the conclusion seemed almost a fantasy. Einstein’s thought experiment had discerned that there was no way for a person to distinguish if they are in a rocket controlled elevator, or under the influence of the gravity from a planet. At face value, the conclusions would seem to be this: since I can’t tell the difference between gravity and a rocket, maybe gravity isn’t real at all.

Any normal person might throw up their hands in exasperation and decide this discussion of the Equivalence Principle is nonsense and go work on something simpler (like brain neurochemistry). But Einstein was a persistent fellow, and pushed a little harder.  He asked, “Is this the real life? Is this just fantasy?” Could it really be the case that there is no way to tell if you are in a gravitational field? What can we experience — what can we observe — that convinces us that we are caught in the grip of gravity?

We understand the world through experiments; they are the medium by which we observe. All experiments — thought experiments in particular — are recipes. Experiments produce results (knowledge about the Cosmos) the same way a recipe produces a cookie. We look at that result, and we ask ourselves a few fundamental questions — they are the same for physics experiments as cookies. Why is the result this way? Can I change what went into the result? Will I get a different result if I change what I put in?

Science and baking are both built around experiments that seek to discover what small changes reveal about the world. In cookies, a relatively small change can change a chocolate cookie into an almost identical vanilla cookie (TOP). A more substantial but not completely different approach might make a peanut butter cookie (BOTTOM). But getting a chocolate chip cookie (RIGHT) takes a completely different approach. [Photo by S. Larson; I don’t know what happened to these cookies after the #science was done; sorry.]

Science is a game of tearing apart ideas and seeing what makes them tick. Changing the assumptions, the recipe of the experiment, could change the outcome. So once again, Einstein returned to our thought experiment with the elevators, and imagined something new. There is a big assumption hidden in our thought experiment — the rooms you and I were confined to were “small.”

Why should that matter? Let’s imagine that our rooms were larger — much larger — and consider each of them in turn.

First, think about your room, on a spaceship. This is a BIG spaceship, of the sort that only the Galactic Empire has the metal and economic resources to build. The entire bottom of the spaceship is covered by rockets, all of them pushing with the same force to make you go.  Now conduct the apple dropping experiment again, first at one end of the spaceship, and then at the other end, very far away.  Both apple drops show the same thing — the apple falls directly down, parallel to the walls of your spaceship.

No matter how large you make a room, if it is being propelled uniformly by rockets, apples all over the room fall straight to the floor, along paths that are everywhere parallel to one another.

Now think about my room, on the planet Earth. This is a BIG room, far larger than any room ever built as it is large enough that if my floors are flat, the curvature of the Earth falls away from under my room at both ends (though I am not aware of this — no windows, right?). If I drop my apple at either end of my huge room I make an astonishing discovery — my apple does not fall parallel to the wall! It lands farther from the wall than it started. Given the outcome of my experiment, I could imagine all sorts of plausible explanations.

Perhaps the walls of my gigantic room are repulsive.

Maybe the walls are repulsive!

That’s an interesting idea; maybe it’s true, maybe it’s not. Can I test it?

Sure!  I build a few new walls at different places in the big room and drop many apples many times. What I find is this: if a wall is closer to the center of the room, a dropped apple falls closer to straight down. At the exact center of the room, two apples fall straight down and land the same distance apart as when they were released. Two apples dropped at opposite ends of the room are closer together when they land on the floor! Physicists get grandiloquent about this and call it “tidal deviation.”

What is going on? The walls clearly aren’t repulsive — a wall in the center of the room doesn’t push apples away from it at all.  We have talked about the lines of force that show the gravitational field.  The gravitational field always points to the center of the source of gravity. What this experiment seems to show is that if my room is big enough, I can detect the shape of the gravitational field!

(TOP) When my apples are dropped, their paths are not parallel; we say there is a tidal deviation between the paths. This is a key experimental signature of gravity. (BOTTOM) We can understand the tidal deviation of the apple paths if we imagine they are following the lines of force in the gravitational field (this is how Newton would have explained it). But this is not the only way to explain gravity!

This idea of the shape of the gravitational field, and its relation to the motion of falling objects, would be a key part of Einstein’s mathematical development of general relativity: it led him to the thought that motion and geometry could be connected.

That may seem like an odd thought, but the fundamental building blocks of elementary geometry are exactly the elements of motion that we discovered in our Giant Room Apple Dropping Experiments: lines can be parallel or not parallel. Einstein recognized that was important, so he explored it. We can too! Let’s think about a flat table top.

If I have two Matchbox cars on my table, and give them a push, they travel in a straight line and never stop (in the absence of friction — every little kid’s dream!).  If I take those two cars and set them in motion  exactly parallel to one another, what happens? The two cars speed off across the table and their paths never cross, no matter how far they go. In many ways, this example is like our two apples on opposite ends of the Gigantic Rocket-Propelled Room — the apples both started falling on straight lines, parallel to each other, and they ended up hitting the floor falling on straight lines that were still parallel to each other.

On a flat surface, two lines that begin parallel stay parallel, no matter how far you extend the lines across the surface.

So this leads to the inevitable question: is there a way in geometry to make the Matchbox cars start out along parallel paths, but ultimately draw closer together? This would be analogous to the Gigantic Room the size of Earth, where apples dropped on opposite ends of the room landed closer together.  As it turns out, the answer to this question is YES.

Imagine a sphere, like a playground ball or a desk globe.  The surface of the globe is two dimensional, just like the table top — there are only two directions you can go: front-back, or left-right. Suppose I take my two cars and set them on the equator in different spots, but both are initially travelling due north — the paths are parallel! What happens? Eventually, the paths of the two cars get closer together, and if we wait long enough, they cross.

If two travellers start at the equator travelling due north, their paths are initially parallel. By the time they reach the top of the globe, their paths cross each other — the paths don’t remain parallel because of the curvature of the globe!

Now, that is no way for parallel lines to behave on a piece of flat two-dimensional paper, but it is perfectly acceptable on a two-dimensional curved surface. THIS is the watershed idea of general relativity — maybe we can describe gravity as curvature. Maybe we can replace the concept of a gravitational force with the idea of particles moving on a curved surface — on flat surfaces, motion along parallel paths stay parallel, but on curved surfaces initially parallel pathways can converge and cross.

Neat idea. But curvature of what?!

Different ways we have devised to measure space or time.

Einstein brilliantly deduced that since our concern is with the motion of things, it should be curvature of the quantities that we use to describe motion — space and time. Special relativity, which motivated our reconsideration of gravity, was wholly focused on how we measure space and time, and Einstein’s former professor, Hermann Minkowski, had discovered that individually space and time are artificial elements of a single medium — spacetime.  Spacetime is the fabric of the Cosmos, the medium on which all things move. Einstein had become well versed in this notion, and concluded:

Gravity is the curvature of spacetime.

This is the heart of general relativity. So how does it work? General relativity is summarized mathematically by 10 coupled, non-linear, partial differential equations known as the Einstein Field Equations, succinctly written as

Fortunately for us, this mathematics can be captured in a simple, two-line mantra to guide intuition:

Space tells matter how to move.

Matter tells space how to curve.

In geometric gravity — general relativity — you can imagine spacetime like a large, deformable sheet. A particle can move anywhere on that sheet, so long as it stays on the sheet.  In places where the sheet is flat (“flat space”) the particle moves in an absolutely straight line.

But what happens if a particle encounters a large depression on the sheet? The only rule is the particle has to stay in contact with the sheet. It continues to travel in the straightest line it can, but if its path dips down into the depression, the direction the particle is travelling is slightly altered, such that when it emerges on the far side, it is travelling in a new direction that is not parallel to its original course!  Space tells matter how to move, with its shape.

Far from sources of gravity (edges of the sheet) spacetime is flat, and objects travel on straight lines. Small masses warp spacetime into a gravitational well (left dimple), while larger masses make larger gravitational wells (right dimple). If a particle comes close to a gravitational well, the curvature of spacetime bends its pathway. If a particle gets trapped in a gravitational well, the curvature of spacetime forces it to travel on a closed pathway — an orbit.

How do you curve spacetime?  With matter. The large, deformable sheet of spacetime is dimpled wherever there is a large concentration of mass; the larger the mass, the larger the dimple. Matter tells space how to curve, with its mass.  The larger the dimple, the larger deflection a particle passing nearby will feel. This at last, is the long awaited connection to the way we think about Newtonian gravity — the source of gravity is always matter, as we expected.

So we have done away with the concept of a “gravitational force field” and replaced it with the idea of “motion on a curved spacetime.” An astute reader will ask a pertinent question: if general relativity is really the way gravity works, why didn’t we discover it first? Where did Newtonian gravity come from?

Both Newtonian gravity and general relativity make exactly the same predictions when gravity is weak and speeds are slow.  In fact, mathematically, general relativity looks just like Newtonian gravity at slow speeds and in weak gravity. These are precisely the conditions we encounter in the solar system, which is why Newtonian gravity was discovered first, instead of general relativity!

You may have encountered models of spacetime gravitational wells out in the world. This one, in the Milwaukee Airport, captures coins for a museum. [Photo by K. Breivik]

It’s fine, of course, to make up a new idea about gravity. But this is science — fancy theories are only as good as the tests that can be conducted to verify them.  Einstein knew this, and proposed a series of tests for general relativity, which we’ll talk about next time.

PS: I rather enjoyed using Bohemian Rhapsody to start this bit of the General Relativity story. It was written by the great Freddie Mercury for Queen’s 1975 album, “A Night at the Opera.” As we shall see in our next installment, Mercury (the planet) plays an important role in bringing the importance of General Relativity to the attention of the scientific community, just like Mercury (Freddie) helped me explain it here. 🙂

PPS: This week I couldn’t capture all of this in one 3 minute video, so I tried to do it in two.

—————————————

This post is part of an ongoing series written for the General Relativity Centennial, celebrating 100 years of gravity (1915-2015).  You can find the first post in the series, with links to the successive posts in this series here: http://wp.me/p19G0g-ru.

First Light

by Shane L. Larson

In the fall of this year, I turned 43 years old.  Four days after my birthday I participated in a long standing tradition that has been handed down through many generations.  It began 403 years ago, on a cool autumn evening in Padua, Italy. Galileo Galilei, then 45 years old, had crafted a simple telescope after hearing of the “spyglass” invented by the Dutch.  Galileo was the first person to turn his telescope toward the sky, letting starlight flit through the shaped lenses and, for the first time, fall on human eyes.  First light.  Galileo beheld a Cosmos full of unexpected wonders, startling revelations, and new mysteries.  Sweeping the faint glow of the Milky Way, easily visible in those bygone days before urban lighting, he discovered it was comprised of innumerable stars — more than he could sketch!  He could see roughness and surface detail on the Moon, which up to that time had been thought to be perfectly smooth. Much to his surprise, he discovered that Venus had phases, like the Moon. And perhaps most importantly, he saw bright points of lights orbiting Jupiter — Galileo was the first person to discover other worlds in the Cosmos.

One of Galileo’s early telescopes.

Today, the heavens are more well known than they were 400 years ago, but still filled with grandeur, mystery, and awesome spectacle. Astronomy is an endeavour pursued by professionals, but also enjoyed by millions of amateurs worldwide, enabled by easy access to telescopes that Galileo would have loved to spend a few long evenings with, sweeping the heavens.  For professionals and amateurs alike, we still celebrate the ritual of a telescope’s first night out under the stars.

First light. It is a magical time for any telescope — the first time it gathers starlight, and rather than let that light be absorbed by the Earth and pass into oblivion, it redirects it to a human eye, carrying the tales of the far away Cosmos.  On a cool autumn evening, nestled down amongst the mountains of northern Utah, I turned a new telescope skyward for the first time. First light.  The telescope was one of my own making, which I built based on the wisdom of others who had built telescopes before me, much like Galileo.  I named it Cosmos Mariner.

My two telescopes. “Equinox” on the left, and “Cosmos Mariner” on the right.

Mariner is much larger than Galileo’s original telescope, and its optical elements were fabricated with higher precision than Galileo could have hoped to achieve in those early days.  All told, Cosmos Mariner will gather about 500 times more light than Galileo’s original telescope, and can see objects about 25,000 times fainter than Galileo.  And what awesome spectacles we beheld!

The first sight of the sky was the double star Albireo.  The “head” of the constellation Cygnus, the Swan, Albireo lies nearly overhead as darkness falls at this time of year. It is a beautiful stellar pair, notable because it shows a striking amount of color — one star glows with a deep, yellow hue, while the other appears as a brilliant blue.  My six year old daughter dutifully climbed the ladder, participating in this special night but perhaps not really knowing what to expect.  She leaned over to the eyepiece and peered in.  Through the gathering darkness, I heard her exclaim: “Pop! They have colors!”  I could have quit then; First Light was a success.  I often think back to that first night when Galileo turned his telescope to the sky for the first time.  What did he look at?  Was he by himself, or was someone there with him to share in the wonder and the spectacle?

The double star, Albireo (beta Cygni).

Our next stop was nearby, off the wing tip of Cygnus.  There, nestled against the backdrop of the star studded Milky Way, a telescope will reveal the faint, gossamer light of the Veil Nebula.  Peering through Mariner’s great eye, we could see faint tendrils and thin tracers of light, woven together in an intricate web of gas.  The Veil Nebula is part of a much greater complex in the sky called the Cygnus Loop.  It is a supernova remnant — the gaseous remains of a star that died in a titanic explosion some 8000 years ago.  It is a doleful reminder that the stars also die, but that the Cosmos is beautiful and delicate even during the throes of destruction.  The death of the stars is the beginning of new birth in the Cosmos — supernova explosions create the complex chemical elements that make up worlds like the Earth and beings like you and I.  The gas and dust that we see today as the Veil Nebula will someday merge with other vast clouds in the Milky Way and collapse under gravity’s inexorable pull until it explodes with the birth a thousand new suns.

The eastern portion of the Veil Nebula.

Our last stop of the evening was high in the eastern sky, nestled just below the neck of Pegasus.  Turning Mariner’s gaze toward that distant corner of the sky revealed the diaphanous glow of a galaxy that astronomers call NGC 7448.  Mariner revealed a faint, glowing oval of light with a brighter orb of luminosity embedded at its center — a spiral galaxy, not unlike our own home, the Milky Way.  There are other brighter galaxies in the sky to see, but on this night I wanted to see this galaxy, because the light from that distant island of stars left its home 100 million years ago, departing for Earth at a time when dinosaurs still roamed our small blue world.  It astonishes me still that I can just now capture that light tonight, drinking in the photons through my eyes, and converting them into evanescent memories.

The spiral galaxy, NGC 7448, 100 million light years away from Earth.

The telescope is magic in its rarest and purest form, a device brought to life by human ingenuity and creativity.  Telescopes expand our vision beyond the small confines of our world to distant corners of the Cosmos, showing us vistas that challenge the boundaries of ordinary human comprehension and force us to think deeply about our place in the grand design.

The great secret of telescopes is that they all will show you more of the Cosmos than your eyes alone will.  The cheap pair of $10 binoculars you have under the seat of your car is a far superior astronomical instrument than Galileo’s original telescope.  For the cost of two or three months of your cell phone bill, you can own a 6-inch telescope that will reveal thousands of distant galaxies, swirling nebulae, the enigmatic surface of Mars, and the beautiful choreography of binary stars.  Large telescopes, like Mariner, are becoming more and more common, providing views that would have made Galileo swoon.

Take a moment tonight, and go out and look at the stars.  Turn off your back porch light, and drink in the starlight that has been hurtling toward the Earth since before you were born.  Make your own First Light, and ponder the deep connection we share with the Cosmos.  And if you’re ever in my neck of the woods, let me know; we’ll pull Mariner out and celebrate in the starlight together.

September’s prompt: “headlines”

This is it!  A new academic year, and a new series of prompts.  Let’s begin this month with “headlines.”  This is derived out of Shane’s demonstration of writing an efficient piece that would work as a newspaper article.  So, while there are no rules, I think we should score extra points for general readability and low word count, say 500-750 words.  Pick a headline or topic and see how to really make it meaningful.  Double extra bonus points for those who can make it especially engaging, although I think this is a given goal for this group.

water

The theme for April is “water,” courtesy of Stacy.

Personally, I’m still working on my March post. Where did the days go?

writing prompt: memory

I almost forgot to post this: Our prompt from Shane for March 2011 is “memory”.

February Prompt: “I am a scientist because . . .”

January Prompt – sustainability

go!

December’s prompt is … music!

As the title says, December’s prompt is music.

design

Here’s the first prompt. A writing submission for this topic is due by the end of November. Questions or issues or clarifications? Just comment on this post and then everyone should be able to see.

My prompt for November: “Design”.

That’s it. I imagine other prompts will be more specific. There’s no other guidance nor regulation. Write something, anytime during the month, and the rest of us get to read, enjoy, and comment. Your post should be in the category “design,” with any tags you choose. This keeps things organized.

I have to admit that I already have something in mind for this, but I guess this is where most prompts will come from.

I propose that we have Brad assign the prompt for December, continuing in alphabetical order of first names. This further justifies why I, Adam, get to go first.