Dare Mighty Things

by Shane L. Larson

In an age of short video reels, endless scrolling through social media, and fractured multi-tasking attention spans, there is a tendency to reduce our civilization — who we are, what we do, what we have accomplished, and what we hope for — to soundbites.  All too often, we look at the world around us, and reduce everything to a single, absolute bottom line; it has a paralyzing and depressing effect on us as a society. Perhaps even more paralyzing is when we are faced with human tragedies and conflicts, presented in a similar endless stream of tiny soundbites. The endless bombardment makes it feel like there is a tidal wave of woe consuming us, our society, and our planet. This bombardment inspires our survival instincts and triggers our fear responses. It feels imperative to fight or hide, but more importantly it feels wrong to think about and talk about better days.

There are threats to be sure. The urge to turn our sight inward is very real.  We become adverse to risk.  We become cautious in everything that we do.  We fear to fail.  The net sum of all of this: we are resistant to speculating or dreaming about the future.

But sometimes we whole-heartedly resist the crushing pressures of a struggling world, and we dare to dream impossible dreams. This is perhaps nowhere more evident than when we consider the space program. 

The NASA Brand

I would argue there is not a brand name in the world that has as much street cred as NASA. Nike? Old Navy? Droid? Apple? Pace Picante sauce?  Please. These brands are all amateurs compared to NASA.  Almost unfailingly, NASA is one of the few entities in our society that garners almost universal admiration. You see kids (and grown ups!) on the street in NASA T-shirts. School supplies are foiled in glitter and color-shifting images lifted from the diagrams from Mars rovers, space stations, and Apollo. When an astronaut comes to town to talk, the seats are filled to the back of the room. When a TV show needs to represent big brains, they posit a character from NASA. When you want to humblebrag about how good your niece is doing in college, you cheerfully relay that she’s working on a project with NASA. When you purvey the news, the good news on any given day is the latest picture from NASA of some faraway place in a remote corner of the Universe doing something humans think of as astonishing.

NASA branded merchandise competes easily with superheroes and movies in the open market. [Images: S. Larson]

How does NASA have this reputation? Perhaps more than any other organization on the planet, they are under the microscope. It is difficult to find people who have not banked awe, dreams, imagination and wonder with NASA. We all know the Big Brains live and work at NASA; when the Big Disaster is coming, NASA will be there to pull out the Big Brains and figure out how to save us (though in Hollywood, sometimes they also need Bruce Willis to help out). The coins that NASA uses as currency are deep thinking, solving impossible problems, and wonderment.

The JPL motto is the first thing you see when you visit the Jet Propulsion Laboratory. [Image: S. Larson]

To my mind, NASA’s reputation is built around two fundamental principles. One is the Jet Propulsion Laboratory’s famous motto: Dare mighty things. The other is use our brains for humanity. NASA’s official motto is “For the Benefit of All.”  The pathway to the future is paved by diligent and unrelenting observance of the facts and data, and using our ingenuity to work through whatever problems we may face. As Mark Watney famously said in The Martian: “You solve one problem… and you solve the next one… and then the next.”

But why do we have NASA? And why do we need NASA doing what NASA does?

Costs & Benefits

If you remember your days in high school and college, you probably spent an afternoon in an economics class, where your instructor told you about “cost-benefit analysis.” It certainly is a principle that drives business decisions, but it is one you use every day in your life as well. The basic idea is that for anything — spending money, deciding to take on a task, or engaging in an activity — you do an internal self-check. You ask what is it going to “cost” you, in time or resources or money or impact on your life. Then you weigh that against the “benefit” to you, what you will gain after all is said and done.

Where does the money that NASA spends go? You’ll see charts and spreadsheets with dollars attached to missions, as if we are duct-taping wads of cash on a rocket and launching it into orbit. But the dollars that we dedicate to NASA and its mission all get spent here on Earth. It pays for every person who works in the NASA workforce, from the custodial staff at the space centers, to administrative assistants processing payroll, to the welders making titanium into spacecraft, to the orbital engineers insuring the satellite orbits for our communications system are good, to engineers designing new digital camera chips, to scientists studying asteroids flying by the Earth, to programmers making computers talk together across the world. Moreover, the money get spent driving the economy here on Earth. NASA doesn’t own an aluminum mine it uses for spacecraft — they pay an aluminum company that pays their workforce to mine and process the material, then they pay a long haul trucker to deliver it to NASA. NASA doesn’t manufacture all their computers and microchips on spacecraft circuit boards — they buy them from vendors, just like you and I. Every dollar NASA spends gets spent here on this blue marble we call Earth.

For its entire history, NASA has had industry partners who build the machines and share the technical work of making us a civilization with access to space. [Images: Wikimedia Commons]

Much has been made about shifting our space program to “private industry.” This is, in many ways, a red herring. NASA has always worked in partnership with private industry. North American built the Apollo Command Module and Grumman built the Lunar Lander. Rockwell International built the Space Shuttles, and Thiokol built the shuttle’s solid rocket boosters.  The United Launch Alliance, a combined effort of Boeing and Lockheed-Martin, build the Atlas rockets that have been mainstay launch vehicles since the 1950s. Private industry has always been part of the space program, but NASA has always been there, like a guiding parent, making sure safely is maintained, corners are not cut, and that the product paid for by you and I is a product that is of the highest quality, of the most inspirational value, of the highest technical capability, and is delivered without cutting corners or breaking promises.

Examples of the work industry has done over the past many decades, in partnership with NASA. Clockwise from upper left: North American constructed the Apollo Command Modules; Grumman built the Lunar Modules; Thiokol built the shuttle solid-rocket boosters; and Rockwell International constructed the Space Shuttle Orbiter fleet. [Images: NASA]

It is never perfect; no technical endeavor is. When the Hubble mirror was flawed, corrective optics and software were developed by NASA to overcome the flaw, leading to more than three decades of the most astonishing and productive scientific returns in human history. Not only was our understanding of the Universe and our place in it expanded immeasurably, but the self-same corrective technology NASA designed for a telescope has merged back into society and is now used for medical imaging and improved mammograms. Similarly, NASA developed the silica thermal tile system that protected the space shuttles on 133 flights. The system failed on STS-107, when a debris strike damaged tiles on the space shuttle Columbia, leading to the loss of the orbiter and crew on their return to Earth. But today, the manufacturing methods for the tiles have extended into other highly porous materials, and are used as heat shields in applications ranging from safekeeping home valuables in residential fires, protecting NASCAR drivers, to providing non-asbestos work surfaces for jewelers. You have wireless headphones because NASA needed astronauts in space to not be tethered by cords for communications. Memory foam came from developing the foam in pilots’ seats. Silver ion technology in water purification systems which inhibits microorganisms like legionella, was originally developed by NASA for spacecraft water systems.

There are thousands of unseen ways NASA has changed your life. NASA (with their industry partners) builds the technology to take us to space, but in the end it all comes back to change our lives here on Earth.

NASA’s budget in the early 2020s has hovered around 22 billion dollars annually. By comparison, the American movie box office revenue for the last couple of decades has floated around 10 billion dollars per year.  Similarly, in the United States, roast coffee revenues are around 70 billion dollars per year, and instant coffee revenue is about 13 billion dollars per year.  Similar amounts of revenues were seen for soft-drinks. Music streaming revenue is nearly 14 billion dollars, and on demand video streaming is nearly 44 billion. [You can explore statistics at sites like Statista. There is strength in data.]

The amount of money, per citizen, spent on NASA is minuscule compared to the money we spend on all other things, but the returns and the benefits are inestimable.

Dream a Little Dream

I grew up in the Rocky Mountains and the American West, from Colorado to Oregon to Montana.  I spent a decade living on the shores of Lake Michigan. Today, I live in the Adirondacks of northern New York. I’ve walked the deep forests, reveled in the roaring spray of mountain waterfalls, peered over the precipice of vast canyons carved from the stone of the Earth, and stood in darkened mountain meadows soaking up starlight billions of years old. These immersions with Nature remind us that we are part of something larger than ourselves. In as much as you and I can take a stroll through a local city park, or go camping in the nearby countryside, or make a family expedition to the National Parks, almost none of us will ever travel to space. 

The Adirondacks in the fall, one small corner of the Cosmos, seen from the surface of the Earth instead of from outer space. [Image: S. Larson]

None of us will ever walk on the dusty deserts of the Moon, or let the sands of Mars sift through our fingers, nor watch the volcanoes of Io explode in eruptions that expand to hundreds of kilometers over the otherworldly landscape.  That’s what we have NASA for — to make those expeditions, to make those discoveries, to send those pictures home to Earth to remind us all that we are part of something  far greater than our ills and our pains and our failures and our struggles, to remind us that there is a better tomorrow to get up in the morning and keep fighting for.

The Earth and the Moon together in space, seen from the Orion spacecraft. Only Artemis astronauts will see this with their own eyes, but NASA is there so you and I can own these sights too. [Image: NASA Artemis program]

There is something to be said for the discovery and exploration of beautiful places. It lifts the spirit, and it makes all those other valuable commodities — food, shelter, security, economy — worth striving for.

There is a famous psychological shift that astronauts experience, called the overview effect, where seeing the Earth from space as a whole planet, without boundaries and borders, transforms their thinking about our collective existence as a species and civilization, and about the intense need to preserve the Earth. As the great author Ray Bradbury once commented in a 1996 interview, “Space travel is life-enhancing, and anything that’s life-enhancing is worth doing. It makes you want to live forever.”

So one last reason we have NASA is so all of us can dream a little dream, for the sake of dreaming. Remember all that we can be, because it makes what you do every day easier to bear.  If you hold anything to be true on the Internet, then take this repeated Serbian proverb to be true: “Be humble, for you are made of earth. Be noble, for you are made of stars.”

Action

Among the myriad cataclysmic happenings in the United States today, it has been widely reported (Big Think;  Planetary Society;  Wired ) that the current administration is poised to roundly curtail NASA and hamstring US capabilities in space for decades into the future. One of the most skilled and technical workforces, which has taken decades to build and curate, is being decimated, and bright young minds whose ardor and passion for a bright future are being scuttled. There are plans afoot to deprecate and decommission facilities and missions that have already been built and are operational, and deliver critical data and support to our modern society (for example, our Earth-monitoring satellite system). 

A report has just been delivered by a Congressional Committee that NASA’s core function and mission is being thoughtlessly destroyed. There are similar challenges to the United States other flagship research entity, the National Science Foundation (for example, see this analysis from Forbes).

In the morass of the US federal budgeting process, each of us has a role to play, and that is to speak with our elected representatives. The Congress decides the final form of the US Budget every year, including what the federal agencies spend and are supposed to do. In many instances, those members of Congress and their staff are ordinary folks, just like you, and need your input about if and why you think activities like NASA are important to our well-being and our future. Reach out to them, and let them know what you are thinking. They assume silence means you don’t care.

You can find the contact information for your government representatives here. You’ll find their contact information, and most of their webpages have electronic forms for sending them your concerns and opinions.

A good resource for specifically helping to ensure NASA’s mission into the future can be found here.

At the time of this writing, the United States government has entered the first day of a federal shutdown that could persist for unknown lengths of time. The federal workforce may be furloughed, but you and I are not. We owe it to ourselves to be vocal, even in these shadowy times, to ensure a brighter tomorrow. We owe it to the future that we do not let the hard-fought assets of our technical workforce and guiding organizations be be frivolously decimated and thrown away. There are far too many challenges facing our society and our planet for that talent and resource to be wasted or ignored.

As Carl Sagan noted in his book Pale Blue Dot,  “For practical reasons, we cannot live too much in fantasyland. Science has taught us that, because we have a talent for deceiving ourselves, subjectivity may not freely reign. Most people eventually come to grips with reality, and find ways to accommodate to the Universe – especially when given the tools to think straight.”  This is the gift the space age has given to our small planet, through the efforts of NASA and space agencies around the world. We have the tools to think straight — let us stare into the harsh light of current affairs, and remember the promise of what lies on the other side.

The Circle of Life

by Shane L. Larson

For most of our lives, we live day to day surrounded by family, friends, colleagues, and acquaintances. Whether we share only brief hellos, a quick text message, or long conversations at sidewalk cafes, we part easily with the unspoken expectation that we will see each other again, sooner or later.

But always, these moments of togetherness come to an end — for each of us, Death lies unavoidably to the future, the completion of our transit around  the Circle of Life. Sometimes it comes unexpectedly, and sometimes it comes with bittersweet foresight, but it comes none-the-less. Inexorably and implacably.

For a little while now, it seems, my life and the lives around me have been punctuated with many of those final partings: the loss of my dearly loved cousin, the passing of a friend’s mother, scientific colleagues passing away, the unexpected loss of a friend from graduate school, and many others. 

They seem to pop up one after another, without respite in between.

This is, of course, a random process, so I should not be surprised, but in the end, it just feels like your spirit is reeling, and another sad bit of news rolls in, keeping the roller coaster of emotions alive. It is, as they say, part of the human condition. It carries deep personal grief for those partings closest to us, and exquisite sadness to watch the burden of grief on others.

There are no balms for the loss we feel when we encounter Death. Our minds must settle into new equilibriums, and our lives into new patterns. We will encounter the spaces that our departed family and friends once occupied, and it is only with startled realization that we remember they are not there. We will include them in our mental dialogues and planned conversations, only belatedly remembering they will not partake in those conversations again. We will talk about them in the present tense, as if they might walk through the door any moment, though we know they will not. We will visit our dearly held memories of them, and laugh at the recollections, before shedding tears when we remember.

But as we all shuffle quietly through grief, and we talk gently with one another, and gingerly creep around memories of the dearly departed, many questions swirl about that often boil down to this:

Is that all there is?

What Are We?

It is clear that humans are different than the other lifeforms we share the Earth with. Or at least our conceit tells us we are. Our genus and species is homo sapiens, Latin for “knowledgeable man” or “wise man.” Taxonomical classification is based on dominant, observable traits that biological organisms have. Acer saccharum literally means “sugar maple” because we  farm sweet syrup from it. The genus and species for platypus is Ornithorhynchus anatinus, which means “duck-like bird-snout,” which seems completely spot on. We name things based on the obvious, observable traits.

But when humans had to name themselves, to distinguish our species from the other creatures of the world, they chose wisdom and knowledge to be the most important character.

Compared to all the other plants and animals and fish and microbes we share the Earth with, we are the only species that we know, with certainty, that thinks about and ponders its existence. We do this collectively as a society, but also as individuals. The most poignant questions about our existence come from asking questions about our isolated, individual selves. 

Each of us lives in our own heads, an ephemeral and gossamer avatar of thought and emotion that is somehow bound to our physical bodies, but feels separate from it. This disconnection is so dramatic that for most of human history, we didn’t know how our sense of being — our consciousness, or what manga comics call your “ghost” and religions call your “soul” — was connected to our physiology at all. Over the last two thousands years, we have come to better understand the role of our brains and hearts in our bodily functions.

But what our consciousness is and how it arises is still a great mystery, in both science and philosophy. But when we think deeply about ourselves, the sooth is that we deem our consciousness most important. Most of us have ears, and kneecaps, and fingerprints. They are all a little bit different, but are not the thing that distinguishes me from you. Not really. What each of us perceives makes us unique is the ghost inside.

And that leads to the inexorable question: what happens to the ghost inside when we reach The End? We know what happens to our bodies — we return to Cosmos from which we came. The iron in our blood and the calcium in our bones discorporates from our bodies and diffuses back into the soil and firmament of the Earth, eventually to be burned away and diffused back into the Cosmos when the Sun dies. But what about the misty incorporeal thing that we think of as “myself?” 

The complexity of the world is still not fully understood, and while the observational fact exists that we are conscious and thinking, we have no experiments that can tell us anything about what happens to that part of ourself when we pass. There are no repeatable experiments that give us any hint of what lies beyond Death for the intangible parts of ourselves. And the truth is, that gives me great comfort. There is grandeur and beauty in the mysteries that Nature still hides from us.

But sometimes someone asks if that scares me? Am I worried about what comes after this thing we call life reaches its terminus? Honestly, I think the answer is no. Because I know we are part of something greater — the Cosmos itself. 

Part of Something Greater

I’m not a religious person, and I cannot in memory recall a time when my ruminations on life included notions of an afterlife. I still think of myself as having a deep spiritual core, connected to believing in our connection to the Cosmos itself. The stuff that we are, in its most inert, raw form, came from the stars. We are, as Carl Sagan so aptly said, are made of starstuff. This is a singular truth that I find most comforting — we all have been part of the Cosmos before, and after we pass from our family and friends and reintegrate with the Cosmos, we will be something again. Some other time. Some other place. Some… other. 

It is the way the Universe works. 

All the Universe knows is that it is, and for our brief time here on Earth, the Universe organized itself to be us, so it could learn, experience, love, feel, and know all the things we know. Everything we have been, are, or ever will be, are part of that great knowing of the Cosmos about itself. 

Here on Earth, we are also part of something greater than ourselves — the human race. It sounds more mundane than being part of the Cosmos itself, but it is no less wondrous and no less remarkable. For all our individualism, we are all part of the greater whole. Humans have been on the Earth a long time — hundreds of thousands of years — but that is a tiny infinitesimal amount of time in the grand sweep of Cosmic history. We have only just been born in Cosmic time, and in our short existence we have, through our impetuous and youthful curiosity, discovered we are part of a greater story. We owe much to the hundred billion humans who have come before us, and have a deep obligation to the unfathomable future of our species.

Yes, our world is fraught with terrible grief and terrible problems of our own making; it is one of the reasons we cling to the idea that we are part of something greater, to avoid the horror that we are nothing more than our tragedies. But we are just children in the Cosmos, and not yet wise. We are still growing up. 

If we do not destroy ourselves, and do not destroy our planet, then we will grow up. One day, in the far future, descendants of ours will look back on the long sweep of human history. They likely will not know me, nor you, nor our loved ones. But the fact that they are alive, standing among all the other wonders of the Universe, they will know that we — We the human race — survived. We used our intellect, and our hearts, and our empathy, and the unknowable glow of our ghosts to learn what We could, solve the problems one by one, and made the world a better place for tomorrow. We recognized that We are part of something far vaster than our meager existence might suggest.

When I Part

There will be, I assume, grief among my family and friends when I pass. Just as I now share grief when people I know depart from life. But I hope through tears everyone celebrates. Because I treasure the time I spend with each of you, and try to open my eyes and see the wonder of the Earth and Cosmos around us, and sponge up as much beauty as knowledge as I can every day, and try to heal what hurts I can, and try to enable each of you to be the spirit you want to be. It is never perfect. Like each of you, I try to do the best I can.

While I embrace science and use it to guide me every day, I think I am wise enough to know the value of other human endeavours as well. Art exists to help us capture in emotionally poignant ways things that are hard to put into words. There are two pieces of art that I carry around, rent-free in my memory, that give me comfort on the long-dark nights when I ponder the end of life.

The first is from the John Cusack movie Serendipity, where Cusack plays Jonathan Trager. His friend Dean writes his obituary in response to an apparently broken heart, saying “The Greeks didn’t believe in obituaries. They only asked one question after a man (sic) died: ‘Did he have passion?’” I cannot discover if this is true trivia about the Greeks, but it resonates deeply with me. Live well now. Love well now. What comes after is for the future, and we know not what it will bring.

The second is from J. Michael Straczynski’s science-fiction opus, Babylon 5, spoken by commander Ivanova when the dead are buried in space. “From the stars we came. To the stars we return, from now until the end of time. We therefore commit these bodies to the deep.” It is a variation of the traditional litany when bodies are committed to the oceans of the Earth, transformed to a future where humans now walk among the stars, but are still very mortal in form. A recognition that we are part of the great Circle of Life that begins in the hearts of the stars.

To all my friends, and family who have gone from this Earth in recent memory, I don’t know if the journey continues or not. But there is an imprint you have left here, effervescent and intangible, though your physical person has returned to the embrace of the mother Cosmos.

From the stars we came, and to the stars we shall return, now and for all eternity. Wherever you are, whatever you may be, I still love you all.

Dangerous Ideas

by Shane L. Larson

There are many ideas in the world. Some are awe-inspiring (“Perhaps we are the only planet with life in all the Cosmos.”). Some are frightening (“What if there were still no vaccine for polio?”).  Some are quite ordinary (“Pads of paper never run out of power, like my iPad.”). Some are quite strange (“What would a Wizard of Oz – Star Wars crossover look like?”).

George Bernard Shaw.

One of the strangest notions to me, however, is that an idea can be dangerous. Uncomfortable to think about? Yes. But dangerous? No.

The notion that an idea can be dangerous is a strange notion to me, because dangerous things should be mitigated to protect me, my children, our society, and our small planet. To my mind, ideas and knowledge don’t fall into the “dangerous” classification.  Instead, I think of ideas like George Bernard Shaw did: “If you have an idea and I have an idea and we exchange these ideas, then each of us will have two ideas.”  Ideas are a commodity, to be considered, grown, used, valued and cherished.

One of my favorite books is a collection of essays edited by John Brockman called, “What is your dangerous idea?”. It is an amazing collection of ideas from notable thought leaders. They take ideas that we may have heard of and push them as far out of shape as one can, turning our normal sense of how things work upside down — what if medicine can control personality? what if we are alone in the Cosmos? what if the fight against global warming is lost? what if our planet is NOT in peril?

I find them all thought provoking, and they inspire a deep sense of reflection about things I take for granted in life or assume are true in today’s modern civilization.

I was thinking in the last week about a pair of essays in this book: one claimed “There are no dangerous ideas,” while the other claimed “All ideas are dangerous.” I discovered that despite my resolute belief there are no dangerous ideas, I found an idea that made me uncomfortable — an idea that could be dangerous. The idea is this: scientists don’t play at politics. This has been a point of much discussion lately as scientists and other academic thought leaders struggle to decide if they have a greater role than just “citizens” in the current turmoil surrounding the American identity.

Avoiding politics is a commonly lauded ideal, often espoused by scientists and engineers, framed by the simple viewpoint that arguing with data is pointless. Science should be pragmatic, quantitative, and data-driven. This is not easily compatible with the rhetorical, emotion-driven, and wheelin’-dealin’ approach often encountered in political endeavors. Arguing without data to inform decisions is an anathema to most scientists. But in reality, scientists and engineers have a great deal to contribute to civic discourse and politics in the world today, because we know things. 

The core strength of “thinking scientifically” about the world is that there is a mechanism by which we can test ideas. We can to the best of our ability set aside our hot-headed emotional selves and make decisions that are informed by evidence and patient measured response to the forces that make the world and society move. The purpose of science is to systematically gather knowledge and understand all the nuances of the amassed understanding that our civilization has compiled, at great cost, over the last few thousand years

Many different complex issues facing humankind are within the purview of science. [Images: Wikimedia Commons]

Scientists have important messages to convey, not just about how science works, but about what science says about the issues of the day.

What can science tell us about how the climate is changing?

What can science tell us about how medicine will change our lives a century from now?

What can science tell us about the dangers to this small world from outer space?

What can science tell us about the interconnectedness of the biosphere? 

What can science tell us about the spread of infectious diseases?

What can science tell us about the likelihood of a mega-earthquake destroying California, or a mega-tornado leveling Omaha, or about another hurricane raging over New Orleans?

Perhaps more intangibly, science offers a stability of thought to emotionally charged and highly polarized conversations. Science can never tell you the right decision to make on a matter of moral or philosophical debate (for example, “should we alter the human genome?” or “should humans take over Mars as their own planet?”). But it can tell you what the important considerations should be, what possible weight to give those considerations, and what the possible outcomes are if a given course of action is taken.

To be clear, the way science works and the way science communicates is at great odds with the normal way information is entrenched in the public and political milieu. In science, we accept that knowledge and our understanding of situations is imperfect, we acknowledge it out loud, and we quantify how imperfect it is — this is not a weakness, it is a strength.

Gavin Aung Than, quoting Phil Plait, quoting Richard Feynman. [Image: Gavin Aung Than, Zen Pencils]

The entire purpose of science is to process information as accurately as possible. The scientific approach investigates some problem, draws conclusions from data, and proposes a course of action. If new data comes to bear, science reevaluates and reformulates what our best practices are. Our old understanding is examined and understood within the context of our new data — what have we learned? Why did we think what we thought before? Is our proposed new thinking consistent with all the data, old and new? Answers and recommendations may change! They are supposed to — flip-flopping is a virtue in science. You learned this when you were taught science — it was called “the scientific method.” Science, as they say, is “a way to not fool ourselves.”

Which brings us back to the possibly dangerous idea. I agree that scientists should not play the game of politics. Modern politics is based on rhetoric, emotion, ideologies, entrenchment, and soundbites. But despite this, scientists should be involved in political discourse. Scientists and engineers are trained to set aside human misgivings and desires about the workings of the world, and think critically about how things work, whether we like the answers or not. They have a nearly unique set of skills to counter illogical swirlings around the challenging issues facing our society today.

Some regard speaking out on issues of science as pontificating — being overly pompous and superior to those who are not trained to think about the world like scientists and engineers. We could certainly approach societal dialogues that way, but it does not serve the purpose of science, which is to improve the lives of humans. Engaging with people outside science and technical fields means scientists and engineers need to not approach conversations the way we would argue with colleagues, but rather the way we approach our classrooms. Our neighbors and leaders and fellow community members have often not been in a science class for decades, and perhaps only took a few science classes as part of their formal education. The goal of talking to them about what we are expert in is not to state what we know, but to help them understand what we know.

So what about the dangerous idea: “scientists don’t play with politics”? If anything, the events of the last year have taught us that we live in a world where rational reasoning are precious commodities, and in short supply when the hearts and the minds of the people are polarized, inflexible, and reduced to accepting and repeating soundbites. There are powerful economic and cultural interests at work, quite often at odds with scientific warnings about the consequences of our actions.  Scientists cannot take a back seat in such a world.

There are plenty of vocal scientists. Some are well known and revered by the general populous, some are quiet well known communicators and teachers in their own fields. Others are villainized by various corners of the political landscape. Despite that, there need to be more vocal scientists — many more. Denial of science is a denial of our birthright, an abandonment of a legacy of 40,000 generations of human beings who have walked before us.

Since January 2025, when the Trump administration came to power, there have been unprecedented attacks and sweeping attempts to dismantle the scientific enterprise in the United States, as well as systems supported by the scientific enterprise, particularly environmental monitoring and health care. The sweeping and careless derailment of our research infrastructure is squandering decades of investment and national effort that have created the modern world. For nearly 80 years, the output of societally funded technical research has made the modern economy, and improved the human condition to levels that would have made our ancestors in the 1800s swoon with envy and amazement. 

The connection between our research infrastructure and the modern world is often difficult to understand, because people do not understand the nature of fundamental research. You can’t build modern technology, or medical procedures, or reliable weather forecasting, or devise advanced computer systems without first understanding the underlying principles of mathematics, physics, chemistry, biology, and geology that govern the natural world. Our high regard for areas of “scientific priority” which may have important economic impact cannot easily advance, make breakthroughs, or have impact on our society without work in other seemingly esoteric areas like mathematics, computational theory, psychology, and sociology.

All modern areas of science, engineering, technology, and medicine are supported by other more fundamental areas of research that do not seem to have direct application to life, society, or economics. [Images: Wikimedia Commons]

You can’t have artificial intelligence without understanding intelligence in biological systems, computational algorithms, mathematical statistics, ethics and philosophy of “free will,” or understanding societal responses to technology.

You can’t have global weather monitoring without a civilian space program, laser ranging, multi-spectrum imaging, computer modeling, and robust historical database management.

You can’t have medical technology that improves the quality of life without chemistry for pharmaceuticals, molecular modeling, biological analogues from the natural world, massive historical health databases, imaging technology from physics, and micro-robotics from engineering. 

You can’t have national security without cryptography, prime number theory, super-scale computing, telescope technology (mounted on satellites), wireless technology and communications, and image processing.

The world today is an ecosystem whose foundation is fundamental technology, engineering, and science. The scaffolding that supports the priorities of our society and governments is not easily seen, nor easily appreciated. Some understand it deeply, and speak about it eloquently. But the people who really understand the foundation are the scientists and engineers who build the foundation, who do the research that is then scooped up and applied to the world in a million different ways. Moreover, our scientists and engineers who are doing their work in colleges and universities are already also engaged in another important endeavour: explaining our work to others. More than anyone else, scientists and engineers have the ability and skill to promote and defend the need for scientific work to the world.

Now is time to wrangle with this supposed dangerous idea: scientists don’t play at politics. Scientific work has become a pawn in the vast milieu of political combat that is absorbing our society. But defending its usefulness and necessity is not “playing politics.” It is promoting the very fundamental viewpoint that the work we do, the knowledge that results, and its applications are for the entirety of society. What we do is for the betterment of the human condition.

It’s time to step things up. 

It is easy to say that. It is not easy to know how to do it. Whatever we do, it will not be perfect, but we cannot wait for it to be perfect. We have to make a good guess, and self-correct along the way — that is, after all, the scientific method. As it turns out, it is what our political leadership is doing, but without the benefit of quantifiable guidance. We must not only talk with our leaders, but we must talk with the rest of the people around us. The world is leaving us behind, to its great peril. 

It’s time to participate.

Why are we paying for THIS?

by Shane L. Larson

Me in my youth. Not that different from how I am now. [Image by Pat Larson]

If you could have talked to my mother before she passed, she would have told you that I was a stereotypical boy — noise with dirt on it. As such, I was responsible for a LOT of mayhem. Science has taught us that young people, particularly young males, are slow to develop. The pre-frontal cortex, the part of the brain that is good at risk assessment,  does not fully develop until the middle of your 20’s or so. What this boils down to is there is a phrase, uttered by my parents over and over again, which perfectly sums up my childhood:

Why are you doing that?

Sure, lots of the things I did could be chalked up to impudence and inexplicable child behavior, but the real reason I was doing it was pure and simple curiosity. I climbed all the way to the top of that cottonwood tree because I wanted to see how far I could see. I was trying to pound a hole through the thin ice at the center of the pond because I wanted to know how thick the ice was. I wanted to know if the flame would follow that trail of “fuel” all the way to the firepit.

Now, I live in the future of my youthful self, and I am a professional scientist. I’m part of a small group of humans who spend their days pondering the nature of gravity and its influence on the Cosmos. I’m a grown-up, getting paid to do a job, but I still get the same question from long ago, from all kinds of people.

Why are you doing that?

It is a question we get asked often in science, and it is often a thinly disguised question masquerading as another question: of what possible benefit is this?  For many branches of science, the answers are perhaps obvious: medical vaccines, climate modeling, energy renewables, solid-state microchips, and a million other avenues of scientific research have easy-to-identify, direct, and important applications to our everyday lives.

In my particular branch of science, at the intersection of gravity and astrophysics, it may seem that understanding black holes, or spacetime curvature, or the death of stars have little to do with your life. Of what possible consequence could they have? The simple answer to that question is “a lot.”

Modern navigation on your phone is an application of GPS technology, which depends on the same mathematics that describes black holes. [Image: S. Larson]

 The tremendous gravitational influences that bend time around black holes are also vitally important around Earth, though their effect is much smaller. The GPS in your phone, which powers navigation and maps every day, functions only because we have a precise understanding of how the Earth bends time in the same (but smaller) way than a black hole. If we had never studied black holes, we would be completely unaware of that effect, making the handheld navigation we enjoy today impossible. In a similar vein, when astronomers observe the death of stars in kilonovae and supernovae explosions, they are monitoring the largest nuclear reaction experiments in the Universe. Measuring the yields and evolution of the elements and radioactive elements produced in the explosions gives us tremendous insights into nuclear physics that is hard to obtain on Earth. That information percolates into our science and technology, and is used in nuclear medicine, nuclear energy, and national defense.

A kilonova explosion is an enormous nuclear processor, remaking stellar material into new elements on a scale that cannot even remotely be approached in Earth laboratories. [Image: NASA-GSFC SVS]

Knowledge, in all its forms, is valuable and applicable in places well beyond where it was first recovered.

But when we look at all the things we do as a society writ large, the question still gets asked: Why are we doing that? Why are we paying for that?

In an age of financial uncertainty, belt-tightening, and political mayhem, everything that we fund collectively as a society falls under attack. When I look at the various things we collectively fund as a society, for each line item I ask myself a simple question: do I care about this? Whether I care or not determines whether the little voices in my head think it is a good use of money or a bad use of money.  Let’s take a little inventory:

I don’t mind funding education and libraries, because I don’t think we want a society full of uneducated people (thanks for that thought, John Green — check this link).

I don’t mind funding roads, because I think the interstate system is better than the muddy twin wagon ruts from the Dark Ages of medieval Europe.

I don’t mind funding emergency rooms, because I think when someone (myself included) gets wheeled in with a piece of steel rebar stuck through them it ought to get fixed, no matter what.

And so on.

Things get muddier when we start talking about things that are more subjective endeavours linked to the human imagination, like art and science.  So I often get asked:

Why should we fund science?

There are, in my mind, three different answers; the total number of different answers to this question is probably as large as the number of scientists on the planet.  But these are my three answers.

The practical.  What has science returned to society? The answer is all the wonders of the modern world. Your quality of life is built on a solid, firm foundation of science applied to your life in the most basic and practical ways. 

Science made the smartphone in your hand, and the computer on your lap. 

Science made your microwave, your antibiotics, the soles of your shoes and the stretchy fabric in your yoga pants. 

Science made the insulation in your house, delivers electricity to the sockets in your wall, and made the vehicle that gets you to work.

 Science made the phone you talk to your parents on, made your refrigerator, and unfailing delivers the NFL to your living room every Monday Night. 

Science made your father’s pacemaker, the contact lenses you are wearing right now, and enabled the bone marrow transplant that saved the life of a little girl down the street from you. 

The same technology that was developed to test the James Webb Space Telescope Mirror has now been flipped around and is used to map eyeballs before surgery.

The Hubble Space Telescope imaging algorithms are now used in mammogram and cancer imaging analysis.

There are myriad ways science drive modern life, like these four examples. Left to right: almost ubiquitous cellular phone technology, precision mechanized farming, pacemakers, and modern contact lenses. [Images: GPL Creative Commons]

There is nothing in your modern life that wasn’t touched by science. Without science, we would still live in caves, we would die in our 20s, and the workings of the world would still be an unfathomable mystery.

Some argue that advanced research is not the responsibility of society, but of industry itself. After all, Apple invented the iPad and is making billions of dollars off of it now, just like Samsung and other computer tablet makers — clearly they can invent stuff. 

But the truth is that you and I paid for the technology that Apple, Google, and Samsung brought together to make the ubiquitous technology we see around us. 

Federally funded research developed GPS, created semiconductor technology at the heart of every microchip, developed early touchscreen technology, and made the first miniaturized digital camera chips. 

All of these things were developed independently of one another over the course of a couple of decades, without knowing how they might be used, and released into the wild. After years of percolation, the engineers at our tech companies saw the potential, and married them all together to create the smart devices that drive your life and a huge fraction of our economy today. All from a comparatively small investment on our part (compared to the economic returns)  as a society.

The wonder. Physics Nobel Laureate Steven Weinberg wrote is his cosmology book The First Three Minutes, “The effort to understand the universe is one of the very few things which lifts human life a little above the level of farce and gives it some of the grace of tragedy.” When I was younger, I never understood that. 

The world is full of wonder, every day, completely surrounding and immersing you, if you pay attention. [Images: Shane Larson]

My friends who know me know that I live science out loud and in the full; there is special joy and revelry I glean every day from communing with Nature, figuring out what she is hiding from us, and then explaining that to other people. The simple joy of discovery with science party tricks in my kitchen keeps me up late at night, gets me up early in the morning, and floods my social media posts. Like shining a black light on club soda (the quinine in the soda fluoresces — it collects the UV light, then reradiates it in a a blue color your eye can see). Or how a water bottle can focus sunlight like a magnifying glass. Or how intricately put together a mosquito appears when viewed up close. Where is the tragedy in such simple joys? There is little in the way of tragedy it seems, but perhaps an inkling of the grace and astonishing creativity of Nature.

No, the key to Weinberg’s point is not the tragedy, it is the farce. The greatest inner fear any of us have is that the things we do, the thousand little moments that make up our lives, might be meaningless. We identify with great tragedies because they illuminate the greatness of what we all aspire to be, and shine a harsh light on what we fear we may or may not be. We can imagine the desire for revenge that drives Prospero in Shakespeare’s The Tempest, we aspire to Billy’s tireless loyalty in Where the Red Fern Grows, we wonder what choices we would make when faced with a world overrun by the Walking Dead.

Famous scientists you may or may not know. Left to right: Albert Einstein, who intuited relativity that allows GPS to work; Dorrit Hoeffleit, an expert in variable stars and the compiler of the Yale Bright Star Catalog; Carl Sagan, a planetary scientists who worked on many of the early planetary missions; and Jocelyn Burnell Bell, a radio astronomer who discovered the first pulsar.

We want to be the heroes, to have the grace to stand up and hopefully survive in the face of inexplicable challenges.  This is the heart of science; there is a reason that scientists can and do hold the stature of rock stars — Albert Einstein, Dorrit Hoffleit, Carl Sagan, Jocelyn Bell, and a hundred other names. These are the people who have helped us see, together with every other scientist who has pursued knowledge and returned it to the collective memory of our species. Every bit of information, every speculation, every experiment, every photograph of the deep Cosmos or micrograph of the unseen world — these are the currency of wonder that assure us that what we are doing is not meaningless, but meaningful. Our accomplishments in science not only improve our lives, but they guide us on the road to understanding ourselves and our reason for being here in the Cosmos.

The inspiration. Lastly, one of the most important things people need to experience is a deep and overwhelming sense of wonder about the world. Being confronted by the mystery and grandeur of Nature stimulates curiosity and encourages people to learn more and participate in asking questions about how and why things happen.

For students, I cannot overstate how important it is to keep them engaged with thinking about the world. I have taught and mentored an enormous number of students in my career. While every single one of them has learned some science from me, not every one of them became a scientist. Some now practice law. Some now are teachers. Some now work in government. Some now are scientists, but not in astronomy! All in all, they are all  out in the world, contributing in important ways that each is uniquely qualified to do. And somewhere early in their education, science keep them engaged and interested until they discovered what they wanted and what they were meant to do. The world is an infinitely better place because of them.

For the average person on the street, they are likely for the most part not scientists. Maybe they are auto-mechanics or dentists or 7-11 managers or village mayors — they are all doing work that keeps our communities and our society humming along. Most of them have not been in a classroom for decades. 

But that sense of awe and wonder lurking in the back of their brain stirs a bit when they see a new picture from NASA, or hear about a new result from the Large Hadron Collider. It causes them to learn a little bit about the strategic and methodical way that scientists parse problems and think about the world. 

Why does that matter?

In my heart of hearts, I am a hopeless optimist. I believe fiercely in giving people the tools to gather information and understand what is going on around them. That doesn’t mean people have to be scientists — it means everyone can benefit from harnessing the way science approaches problems and navigates making decisions. Yielding to their curiosity exposes people to the careful consideration of information, teaches them how to gather data, and how to use it to solve problems. And solving problems is how the world becomes a better place.

Frankly, the world is faced with some big damn problems — meeting the needs and demands of a burgeoning population, suppressing virulent diseases and epidemics, escalating climate change, and social injustice that is outlandish for an advanced civilization in the 21st Century. Big damn problems need big damn heroes. Science teaches people how to be big damn heroes.

Science trains and hones the mind, making a person a creative and resourceful problem solver, whether that person stays in science or not.

Science teaches people that problems are solvable, and that there is usually more than one way to solve a problem.

Science shows us what we are capable of, when we set our minds to it.

Some last thoughts. So, why should we fund science? Ultimately, as we’ve seen, there is no single, and perhaps no simple answer. But I think all of it boils down to something simple: science is a tool that improves the human condition. Everything we’ve discussed here points to that.

It is a way of thinking about the world that endeavors to approach problems from a viewpoint of data and facts. It is a framework for making sound decisions. It is a methodology for iterating on tough issues, and slowly improving the outcomes. 

In an age of dumpster fires and doomscrolling, science is a way to understand how we recover. It provides inspiration when the moments are darkest. It provides a reminder that we are part of something larger than ourselves, and that our intellect is the greatest gift the Cosmos has given us.

It is a gift that should not be idly squandered nor ignored.

If dark matter and exoplanets and starling murmations and volcanic lightning inspire people to think more deeply about the world, then its worth every penny we spend. Because we need people to think more deeply about the world and our future in it.

A Forgotten Message

by Shane L. Larson

This month would have been Carl Sagan’s 90th birthday. His birthday could have sidled past, but I dutifully have it on my calendar, along with all my friends’ birthdays. It was a tumultuous week as it went rolling by me, and I started to think about how prescient Sagan was about how we build value systems in our society, sometimes with and sometimes without knowledge. In the last few weeks, people have oft reposted a famous passage from Chapter 2 of “The Demon Haunted World,” where Sagan appears to have had a premonition that captures everything people are feeling right now. 

An often reposted paragraph from Carl Sagan’s “The Demon-Haunted World” (1995). [Image & Highlighting: S. Larson]

Perhaps incongruously with this passage, the chapter is called “Science and Hope”! While I certainly feel all the feels from this passage, there is a forgotten message in all of this that Sagan was always quick to espouse. It is “hope.” Hope for our species and our planet, because we have somehow discovered over the 40,000 generations that we’ve been on this planet that science is a tool to navigate the dangerous waters in which we tread. Not a perfect tool, but a reliable tool.

A small reminder of Carl Sagan and COSMOS that I print and tape in the front of each of my everyday-carry jouranl. [Image: S. Larson]

For many in my generation, our parents, teachers, and mentors used Sagan’s COSMOS as a vehicle to propel our interest in science. Today, I find myself constantly returning to the lyrical poetry of COMSOS as a foundation to renew and sustain my passion not just for science, but for helping people understand the beauty and wonder of the Cosmos around us. It is replete with wonder, awe, prescience, and great quotes. In the front of every one of my daily journals, I tape the opening refrain from the very first episode of COSMOS, as a reminder of why I pursue science, and why we talk to people about science every single day. 

Through the entire COSMOS television series, and through the many books he wrote, Sagan deftly weaves together history of discoveries with stories of trials and tribulations, spinning out the tales of successes and failures of our species. In the end, we are left with an epic survey of what humans are capable of. That message touches something deep and visceral in people. There is one bit in COSMOS that stands out to me as enormously relevant to the world today. In Episode 3, “The Harmony of the Worlds” he comments on what the purpose of science is. In his often poetic but direct way, he speaks a great truth about the Cosmos: “It’s possible to figure things out. We can do science, and with it, we can improve our lives.” (my emphasis added) Why does this particular bit stand out to me? Because it is in stark contrast with the way people often think about their personal relationship or experience with science, and increasingly, how science is often villainized as somehow not being understandable or useful to ordinary folks in their ordinary lives. 

But everyone uses science in their everyday lives, to do everything they need to do. It is perhaps not called science, and may not be science in the form you recognize from your high school or college classroom, but it is science none-the-less. You utilize it in the same way professionals utilize it, to solve problems effectively, efficiently, and with satisfying outcomes. Your formal science education in school certainly helped wire the neurons in your brain to be good at solving problems, but there is an unerring truth here that Sagan so eloquently captured in COSMOS: “It’s possible to figure things out.” Solving problems in your everyday life is doing science, whether you think it is science or not. Why? Because, as it turns out, it’s one of the best ways of doing things, and humans are good at exploiting the best ways of doing things.

There are a limitless number of examples of how “everyday life” and “professional” science work. Perhaps they will give you something to cogitate on, and stimulate discussion at dinner some evening.  Let’s consider two.

To the naked eye, table salt crystals and white sugar crystals are nearly indistinguishable. Even magnified, salt (left) and sugar (right) appear very similar!

Consider the following simple life conundrum. You are going to stir a spoon of sugar into your morning coffee, or perhaps sprinkle it over your cereal, or add it to cinnamon and broil your morning toast. There are two spoons on the kitchen counter, both full of small, granular, white crystals. Do you take the spoon on the left or the spoon on the right? You only get to pick one, because I’m taking the other. At first glance, you may simply grab one and use it. But if you are older than about 7 years old or so, your practical life experiences will give you pause because you know that salt and sugar are both granular white crystals that look the same. You pause because a spoonful of salt will completely ruin your breakfast, whereas a spoonful of sugar is exactly what you want.

So how do you pick a spoon? The way to make this decision is science. You may think the problem suggested here is silly because there is an obvious way to make the decision, and that is good — it means you fundamentally understand the principle of science and its use in life. The way to make a decision is to learn something more about the contents of each spoon, and we have a name for that process: “observation” or “collecting data,” and there are many ways to do that.

Another way to collect data is to “do an experiment.” In this case, that could be as simple as dipping your finger in each spoon and tasting the contents. This will certainly tell you if the spoons are different, but you will only know which one to use if you have had prior experience with “salt” and “sugar.” This last point cannot be stressed enough. The taste of salt or sugar are neither good nor bad — they are simply different. Understanding which one is best for your coffee is a bit of knowledge you have acquired based on previous experiments.

One way to collect data is to “ask an expert.” If I put the spoons out before you walked in the kitchen, then I presumably know what is in each one, so you should ask me. Similarly, if you didn’t know how to make cinnamon toast, you could consult an expert — a cookbook, your aunt who first made it for you, a cooking channel on YouTube, to find out if sugar or salt is best on cinnamon toast. “Experts” are people who have previously collected data about the world, learned what its implications are, and then share that information with others who need the information.

This is how science works, and how you use it (perhaps unconsciously) in your everyday life, to lead your life and improve your day-to-day existence. The conundrum of the salt and sugar spoons is not one that happens often — I certainly have erroneously put salt in place of sugar, perhaps from absent-mindedness or as the victim of a practical joke. But not often. Why? Because science is an iterative process. The first time a problem is solved, a solution is posited or implemented, and we wait to see if the problem happens again. In the case of sugar and salt, we often place them in distinguishable and unique containers: salt in shakers, sugar in a bowl. Most of the time, this prevents the conundrum described above — food doesn’t get ruined, life is greatly improved, and we move into the future.

A simple and common solution to successfully telling sugar (left) and salt (right) apart in the kitchen is to store them in different, unique containers.

There are more serious applications of science to your life that are less… ordinary, and that only become beneficial on long timescales. On a societal level, science is woven into the fabric of our civilization, and nowhere is that more obvious than in healthcare. Where it is available, healthcare has raised life expectancy from around 30 years in the Middle Ages, to about 55 years at the dawn of the 20th Century, to around 80 years today. This is directly attributable to developing an understanding of the microbial origin of disease and how to combat it with treatment like vaccines, to developing an understanding of the impact of diet and nutrition on personal health, and to lifesaving drugs like insulin or technologies like heart stents. The long, slow acquisition of knowledge can only in hindsight be viewed with the understanding of what each discovery meant along the path to helping humanity.

Location of the pancreas in humans. [Image: Wikimedia Commons]

For instance, you have a lot of internal organs. You’ve probably heard of the names of lots of them, but perhaps don’t know what your body uses them for. Consider your pancreas. Most of us have heard of it, but I certainly can’t point to where it is. Some of us may know that cancer of the pancreas is a particularly vicious form of cancer, and survival rates are low. But what is the pancreas?  Our understanding is one that has been long and slow to develop.

The pancreas is a part of your digestive and endocrine systems (your endocrine system makes hormones, all the chemical messengers your body uses to talk to itself). It is nestled down in your mid-abdomen, behind your stomach and under your liver. The discovery of the organ is usually attributed to a Greek surgeon named Herophilus of Chalcedon, who lived around 300 BCE; it was named several hundred years later by another Greek anatomist, Rufus of Ephesus.

Paul Langerhans, a German pathologist, first discovered microscopic structures in the pancreas in 1869, but their purpose and function was unknown. It took until 1889 when Oskar Minkowski, a German physician discovered removing the pancreas from dogs caused them to become diabetic. Even though this firmly linked pancreatic function to diabetes, it wasn’t until 1901 that Eugene Lindsay Opie, an American physicsian, connected the disease to  Langerhans’ structures. It wasn’t until 1922 that this knowledge was connected to the idea that insulin could be extracted and successfully administered to a diabetic patient in Toronto, leading to its widespread use. A complete understanding of the structure and properties of insulin was finally discerned in 1969 by Dorthy Crowfoot Hodgkins, fully 100 years after Langerhans’ originally discovery! Hodgkin had won the 1964 Nobel Prize in Chemistry for her work in using x-rays to understand biochemical substances.

Four scientists who made the connection between body functions, diabetes, and insulin. Left to right: Paul Langerhans, Oskar Minkowski, Eugene Lindsay Opie, and Dorthy Crowfoot Hodgkins.

In one paragraph, I have blurted out more than one-hundred years of discovery, noting only the outcomes, but completely ignoring all the trials, tribulations, confusions, errors, late nights, early mornings, ruined experiments, spilled beakers, wrong pathways, and incremental discoveries that have lead to what is today firmly understood science. Science that has transformed the lives of millions of people. 

We could go on like this for much longer than I have. There are endless objective examples of ways that science and engineering have improved the human condition, some well known, and others not so much so. Refrigeration. Antibiotics. Improved crop yields. GPS navigation. Solar cells. Surgical steel. Eyeglasses. Glowsticks. Heat pumps. Electric generators. Ballpoint pens. Superconductors. Radio communications. Cochlear implants. Laser cat toys. Laser eye surgery. LASERS! The list goes on.

Inexplicably, though, science has become a talking point for political debate. But that does not change the fact that there is objective truth in the Cosmos, and that science is the mechanism to discover and understand that objective truth. One important reason is improving the human condition. I have faith in that ideal, and just as my inspirations in science are cemented by Sagan, my faith in our ability to come together in common human interest is cemented by the oratory of possibly one of the most skilled orators in history, the Reverend Martin Luther King, Jr. who said “I still have faith in the future… I will not join anyone who will say that we still can’t develop a coalition of conscience.”

And so, we marshal on. Pick up your favorite Carl Sagan book, curl up in your reading spot, and remember the forgotten message — that science is the most human of human endeavours, and it is there to make the human condition better. Drown yourself in the Hope of Science.

Happy Birthday, Carl. We’re still trying.

Chasing an Evanescent Cosmos

by Shane L. Larson

Humans have looked at the sky for as long as we have inhabited our small, planetary home. For 40,000 generations we have basked in the warmth of our mother the Sun, watched the Moon hurtle across the sky in an ever-changing succession of phases, and fallen asleep as the stars slowly wheeled overhead in their familiar and comforting constellations.

The familiar shape of Orion, with it’s distinct three belt stars, graces the winter skies in the Northern Hemisphere, as it has for all of recorded human history. [Image: M. Larson (iphone!)]

Our perception of the Cosmos is one of steady and dependable clockwork, changing slowly on the timescales of days or months as the patterns of the constellations shift in slow progression with the seasons, but returning to their familiar places in the sky a year later with dependability. Yes, the sky changes, but never dramatically. On the timescale of human history, it is in many ways a dependable constant. The skies I see tonight are just like the skies my grandparents knew, and their grandparents before them.

Comet NEOWSIE (C/2020 F3) graced the skies of Earth unexpectedly in the summer of 2020, during the Coronavirus Pandemic. Comets are one example of rare, transitory experiences humans can have with astronomy. [Image: S. Larson]

There are, of course, events where the sky changes in remarkable and dramatic ways. A bright comet will suddenly brighten and be visible for a few weeks. A distant star will gasp its last breath, and blow off its atmosphere in a cataclysmic nuclear explosion. And sometimes, the Earth and the Moon in their eternal dance around the Sun, will toss their shadows on one another to give us lunar eclipses and solar eclipses.

Any of these events are dramatic enough to have caused consternation in the course of human history, particularly in the days before humans had begun to dissect the patterns of Nature and use that knowledge to better understand our place and purpose in the Cosmos. 

But you and I live in the future. Many before us, both before the birth of modern science and after, have learned the patterns of the sky to such precision that we can predict when the Moon will spin into the line of sight between us and the Sun, and shed a narrow band of shadow on the Earth — a solar eclipse.

A total solar eclipse occurs when the Moon passes between the Earth and Sun. The Moon’s shadow races across the surface of the Earth, blotting out the Sun for those who stand under the racing shadow. [Illustration by S. Larson]

One such moment was this past week, on 8 April 2024. A total solar eclipse was due to roll ashore on the southern coast of Mexico near Mazatlan, then roll northward into Texas, and track along to the northeast through the midwest of the United States, before passing over the eastern seaboard of Canada and out into the north Atlantic.

The path of the 8 April 2024 total solar eclipse, moving from the southwest to the northeast over North America. The centerline is marked in red; everyone in the grey band was within the path of totality.  [Illustration: S. Larson]

Many of us had been fortunate to see a previous solar eclipse that crossed North America from Oregon to South Carolina in August 2017. I saw that eclipse, and wrote about it both the day before, and the day after!  The response that many of us had was a common one that is almost always expressed as a question: “When can I see another one?!”

The April 2024 eclipse was a remarkable opportunity for many of us who had asked that question. We could travel to the centerline pretty easily, and the duration of the eclipse was going to be longer than in 2017 — almost four and a half minutes, longer than the two minutes and 27 seconds from 2017. It doesn’t sound like much, but some deep part of our soul knows that longer matters. 

That’s because standing in the shadow of the Moon, your mind knows something remarkable is happening, but it is far outside your everyday experience. It is difficult to grasp and hold on to and put into words. You have a lifetime of experience with the Sun — it is steady and reliable and is the same every time you see it. You never see it do something unusual, and your brain knows it.  When the Sun disappears, and is replaced by an inky spot of darkness in the sky, you feel it deep down in your soul, and you want to hold on to that memory and feeling — it is precious.

A message from a friend of mine about the experience of standing in the utter darkness of totality during a solar eclipse. [Shown with permission]

The impetus for many adventures are some friends who are keen on the experience, but want to share it with someone else. Sharing gives you the opportunity to talk afterward, a chance to draw out the gossamer threads and cement those few magical moments in your memory. It was no different for us. It began with a simple plan that was just a few people, but rapidly swelled until we were just a tidge more than 30. Old and young, children and parents, millenials and old hippies. A motley crew that was a skein of linked acquaintances, soon to become a band of friends who experienced one of Nature’s great spectacles together.

But from where? 

A site was selected based on historical weather averages. April is springtime in North America. Along wide swaths of the eclipse track that means turbulent weather, spring rains, occasional snows, and cloudy days as Spring tries to assert herself over Winter. For many, this is a once-in-a-lifetime event, so you play the odds. We, like many others, descended on Texas.  

The historical cloud cover in North America on 8 April, generated from 43 years of data.

We settled on an RV park in the Texas hill country, west of San Antonio, on the banks of the Rio Frio just outside Garner State Park. If you were to pick an awesome site for the eclipse, this was the one.  Right along the centerline. 

We converged on Saturday, two days before the eclipse, and the forecast was looking grim. Predictions for Eclipse Day on Monday were for 90% clouds, possible rain. Quite against all odds, the northern reaches of the eclipse track, historically cloudy in April, were predicting clear skies! 

The cloud forecast from the Washington Post on 5 April, just three days before the eclipse!

The agony of statistics!

There was a lot of hand-wringing around the firepit that evening, and long into the next day. What should we do? Should we stay put? Should we try and drive to clear skies? It was predicted only 50% cloudy three hours north — were those odds we liked? It was predicted only 10% cloudy nine hours north in Arkansas? Did we want to do 18 hours on the road (there and back)? What if we got caught in traffic and missed everything? 

In the end, we decided to stay put. The magic of the moment was being together, and there was still an experience to be had. Even on a cloudy day, it was still going to get unnaturally dark. Maybe we’d get lucky, and maybe we wouldn’t. 

Eclipse day dawned cloudy, as predicted. But Nature is a tease. The clouds were layered, and moving in different directions, and every now and then there was a fabulously clear blue spot, sometimes in front of the Sun — shadows would sharpen and we could feel the warmth on our faces, tantalizing moments of hope.

We had an eclipse talk before the event, to answer questions and help everyone feel like they were prepared. [Image: M. Mesel]

We gathered about an hour-and-a-half before the eclipse, together with more than a hundred people camping at the RV park, and talked about what eclipses are, and how and why they happen. We reviewed how to see the event safely, and made sure everyone had eclipse glasses. And lastly, we talked about what to expect and experience, clouds or not.

Then we all dragged our camping chairs to a wide grassy spot, and waited. The clouds were thick, but there were gaps that dashed across the sky, and moments where we could make the Sun out through the clouds, and other times it stood in the clear sky.  Eclipse glasses pressed tightly to our eyes, we could see the Moon had started the eclipse run and was dutifully eating more and more out of the right side of the Sun.  

Our eclipse expedition crew, waiting for totality on 8 April 2024.

First we could see just a little tentative nibble, and then a cloud would dash in front and obscure the view. But just a tiny bit later, the Sun would emerge again, and joyous cries of amazement would rise up from the sea of chairs as people witnessed the Sun slowly disappear.

Our views of the ongoing eclipse through eclipse glasses (left) and through the cloud layer (right). [Images: S. Larson]

As the last few moments approached, the Sun had become a thin crescent, a mimic of how the Moon sometimes appears. But we could see dark skies ahead. A massively thick cloud was rolling our way, with all possible ill-timing. It was roiling and dark, no breaks to be seen anywhere. It moved in front of the Sun, barely a minute before totality began. 

We could feel the chill on our skin. Was it the ever fading light from the Sun, now obscured? Or was it the cold embrace of weather carried on our nemesis, The Cloud? 

The Cloud, the nemesis of our expedition. [Image: S. Larson]

Totality was approaching, not a break to be seen. Dutifully linked to the digital world, we had GPS times on our phones, and precise knowledge of when Totality should occur, now on the far side of The Cloud. About 20 seconds before Totality, a swelling countdown rolled across the sea of people…

20 – 19 – 18 – 17 – 16 – 15 – 14 – 13 – 12 – 11 – 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 – 1 – 0!

Right on cue, the skies descended to darkness. What was moments before a cloudy day illuminated by dim filtered sunlight, plunged into darkness. People erupted in applause and cries of joy.

Totality descended on us, right on schedule. Dark as night, but it swept over us in mere seconds. [Image: S. Larson]

We strained to see a break in the clouds, but there were none. We looked hither and thither, drinking in the darkness around us. Everyone around was atwitter with things they were noticing, calling them out to everyone else, so we could all share in the moment.

The automatic streetlight at the entrance to the RV park came on. The birds got quiet. Bats started flitting overhead. The humans were still taking pictures. We craned our heads around, and could see that near the horizons, it was still light — realms outside totality, where the light still fell. But where we were, it was dark.

For 4 minutes and 28 seconds, we were in the Shadow of the Moon.

We stood in totality, and could not see the Sun nor the gossamer aura of its corona. But still we stood in the darkness in wonder. [Image: S. Larson]

Together, we basked in  a few moments of darkness. For a few precious minutes, the world did something completely unusual — something our rational minds could process and understand, but something deep down we knew was unusual and different and ephemeral. To share it with friends is an essential part of experiencing the event as humans, so that you can together process and understand what the event emotes within us.

And then, it was over as quickly as it had started. The light rose, and we were once again sitting in a grassy patch on a cloudy spring day, the soft light of the Sun filtered by clouds above. Except we were different. For a long while, we stayed put. Comparing experiences, taking selfies, laughing, and sharing the joy.

Post-eclipse reverie, with friends and song. [Image: Z. Mesel]

Later that night, after normal darkness fell, we sat in a great circle in the middle of the camp, and engaged in another time-honored human tradition of sharing songs and music. Songs of the sky and moonshadows, songs of sharing and family, and songs of learning and travelling home. Picked out on the strings of a guitar, with some voices well-trained and other voices simply happy to be together, we bonded just a little bit more to ensure that we each remembered how special that day had been.

For some of us, there will be other eclipses. Perhaps with clouds, perhaps without. But for all of us, there were four and half ephemeral minutes of darkness that we shared, on the middle of a cloudy day in southern Texas.

An Ephemeral Whisper in the Cosmic Dark

by Shane L. Larson

In a 2012 article in Esquire, the inimitable American magician Teller noted, “Sometimes magic is just someone spending more time on something than anyone else might reasonably expect.” 

This past week, the world was greeted with the news that a worldwide collaboration of scientists, in a multiple collaborations, made a magical announcement: they have detected a faint gravitational hum coming from the Cosmos, created by pairs of super-massive black holes, strewn across the Universe, dancing around each other in slow, languorous orbits that shed gravitational waves. 

An artistic interpretation of an array of pulsars immersed in gravitational waves from a distant supermassive black hole binary. [Image: Aurore Simonnet/NANOGrav Collaboration]

Like most newsflashes from the frontiers of science, the announcement is a magical moment, instilling deep wonder and inspiring an endless barrage of questions about what it means, how was it found, what does it tell us about other mysteries of the Cosmos, and why does it matter to us down here on Earth? The magic and the wonderment stem from the bigger than life nature of the discovery, far removed from the trials and tribulations of day-to-day existence on Earth — a reminder that we are part of something far larger than ourselves. But for the scientists around the world who made the discovery, it’s what Teller said: the discovery is the culmination of decades of work, the result of spending more time on this particular mystery of the Cosmos than anyone else.

Let me tell you three things about this remarkable achievement.

[1] What is a “nanohertz gravitational wave background”?

This tale begins with the idea that nothing in the Universe has to only be found leading solitary monastic lives, drifting along in the vast void. Very often, objects can find each other (or are born together) through their mutual gravitational attraction — this includes, stars, planets, asteroids, galaxies, and as it turns out, black holes.

We know from long, detailed studies of the sky with telescopes two remarkable things.

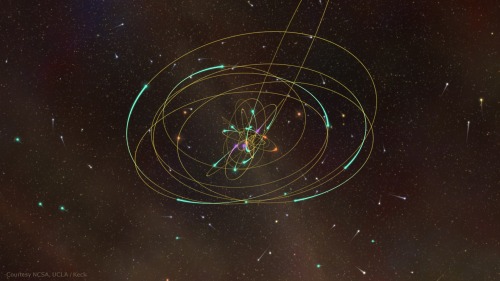
Two decades of observations have shown the orbits of stars around the supermassive black hole at the center of the Milky Way. Observations like these earned Andrea Ghez and Reinhard Genzel their share of the 2020 Nobel Prize in Physics. [NCSA/UCLA/Keck]

First, we know that most galaxies have at their hearts a massive black hole, millions or billions of times more massive than a single star. If you are a science fan, you’ve heard a lot about this recently, from the 2020 Nobel Prize in physics awarded for precise measurements of the enormous black hole at the center of the Milky Way. You have likely also heard of a remarkable picture taken by the Event Horizon Telescope collaboration, showing the silhouette of a massive black hole in the galaxy M87, an inky void against the glowing light of the gas that surrounds and feeds it.

The first picture of the black hole at the heart of M87, formed by light being bent around the inner most regions of space outside the black hole. [Image: Event Horizon Telescope Collaboration]

Second, we know that galaxies collide. One of the most spectacular examples of this are a pair of galaxies known as “The Mice,” slowly tearing one another apart as they merge over the course of a billion years. Another example is a remarkable ring galaxy known as Hoag’s Object, the result of a small galaxy dropping through the heart of a larger companion and leaving a beautiful geometry in place, like the spreading ring from a stone dropped in a pond.

Examples of the consequences of galaxy collisions. (left) A pair of galaxies mid-collision, known as “The Mice”. (right) A ring galaxy known as Hoag’s Object. [Both Images: Hubble/STScI/AURA]

These two bits of knowledge  leads to a lovely question: what happens to the massive black holes in a galaxy when two galaxies merge and combine? The expectation has long been that the black holes would slowly sink to the center of the new combined galaxy, eventually find one another, and merge to become a newer, bigger black hole. That process of finding one another and slowly spiraling together to become one takes a long time.

When the black holes do find one another, they dance around in an orbit, not unlike the orbits of the Moon around the Earth. Long before the black holes make their final crash, those orbits are large and can take many decades to complete. During this time, as they warily spiral around one another, they are constantly changing the parts of the Universe they are bending with their gravity, and that change ripples out through the Cosmos as “gravitational-waves.”

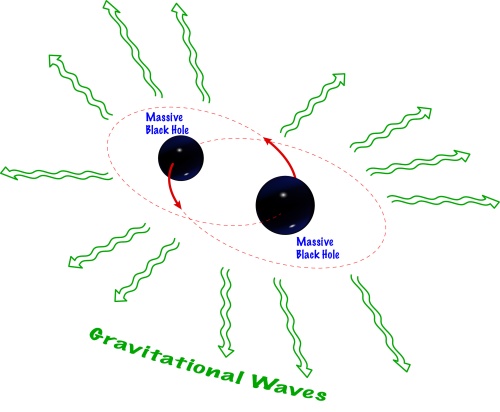
As massive objects orbit one another and get closer and closer together, they emit gravitational waves in all directions. [Image: S. Larson]

Sitting where you and I are sitting in the Cosmos, the gravitational-waves from any one of these black holes will wash through our galaxy, but only one complete wave from the black holes will pass over the course of many years. There are about a billion seconds of time that elapse every 30-ish years; if a complete gravitational wave takes 30 years to pass by, then each second means one-one-billionth of a gravitational wave passes by. Scientists abbreviate the amount of “one-one-billionth” with the word “nano-” which comes from ancient Greek meaning “very small.” Nanohertz gravitational waves are waves so large it takes several decades for them to pass by.

Which brings us to the last word, “background.” This is a bit of scientific jargon, but it describes a phenomena that most of us are likely familiar with. Consider the last time you were out shopping, or at a high-school basketball game, or in a crowded restaurant. Immersed in a crowd of hundreds of people all carrying on conversations and laughing, you were immersed in a cacophony of sound. You could certainly hear the person next to you (with whom you were probably discussing the discovery of the nanohertz gravitational-wave background), but all the other conversations are overlapping and blended into the “background.” The gravitational-wave background is the same way — there are so many pairs of massive black holes strewn across the Cosmos, all of them shedding gravitational waves, that the cacophony of them merges to form a faint hum of indistinguishable signals.

From dark sites far from cities, you can see the Milky Way in the night sky overhead, as in this image over the Pando Forest in Utah. [Image: Shane L. Larson]

This idea of overlapping indistinguishable signals becoming a faint, detectable signature of the Universe is not unknown in astronomy. If you have ever had the good fortune to go camping, far from the glaring lights of our cities, and looked up to see the vast tapestry of the sky over you, you’ve likely seen the river of the Milky Way, arching overhead from one side of the sky to the other. A faint, gossamer glow of light that when you first see it may have reminded you of clouds or fog. But it is no such thing — the Milky Way is the combination of the light of a hundred billion stars in our home galaxy, each too faint to see individually, but together they make a faint light your eye can detect. The gravitational wave background is the same idea, just with gravitational waves instead of light.

[2] How was the nanohertz background detected?

You may have heard of gravitational-wave observatories before (LIGO, and LISA), but this new discovery was made with a remarkable technique known as pulsar timing, where we mesh our own modern technology with natural phenomena from Nature to create a galaxy-spanning gravitational-wave antenna array.

Artist’s rendering of a pulsar – a rapidly rotating neutron star that emits a beam of radio light that passes the Earth once every rotation. This results in a detectable pulse from the star, hence the term pulsar. [Image: Olena Shmahalo/NANOgrav]

It begins with dead stars — stellar skeletons of a particular type called a pulsar. Certain stars, when they reach the end of their lives, explode and leave behind a cinder of their former selves, roughly the size of a city (about 20 kilometers across), but containing the mass of about one-and-a-half times that of our own Sun. Like most things in Nature, these stellar skeletons are rotating. What makes a pulsar “pulse” is it has a very bright beam of radio light it is spewing out of a point on its surface — as it spins, it sweeps that radio beam across the sky, and everyone in the right place sees a bright pulse as the beam goes by, and then nothing, and then a bright pulse, and then nothing — a cosmic lighthouse jetting its signal across the Universe.

Astronomers create pulsar timing arrays (PTAs) by using radio telescopes on Earth to monitor a large collection of pulsars every now and then for decades. Today, there are several such collaborative enterprises on Earth: NANOgrav  in North America, the European PTA in Europe, the Indian PTA in India, the Parkes PTA in Australia, and an overarching global collaboration called the International PTA. Each of these collaborations watches their set of pulsars, and records with exquisite precision what time each of the pulses arrives at Earth.

Because each of the pulsars lived their own lives, in their own little corner of the galaxy, we expect there to be nothing about any of the pulsars that is related between them — in the absence of anything going on, each their signals arrive at Earth at a predicted time defined by the pulsar and where it is relative to Earth. Nothing is correlated (in the literal sense of the word) between the pulsar signals.

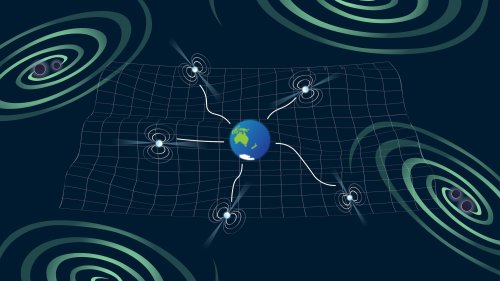
An artist’s impression of a pulsar timing array, immersed in a sea of gravitational waves from supermassive black hole binaries outside the galaxy. [Image: Shanika Galaudage]

However, if you are timing many different pulsars, and a gravitational-wave passes through the galaxy, then a subtle pattern emerges. When a gravitational-wave passes between you and a pulsar, it stretches the distance and then it compresses the distance as the wave passes by. When the distance stretches, it takes longer for the pulsar signal to travel to Earth, and in your timing the pulses seem to arrive late. When the distance compresses, it takes less time for the pulsar signal to arrive at Earth, and in your timing the pulses seem to arrive early. But the magic is this: the gravitational-waves are passing through the Milky Way, and changing the spacetime between us and every single pulsar being timed! That means before, where nothing was expected, there is now a unique and detectable correlation between all the pulsars in the timing array!

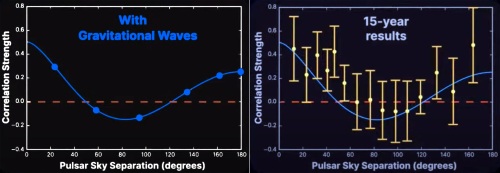
Summary graphs of the results from NANOgrav. The curve shows the correlations between pulsars in the array due to gravitational waves. (left) The red dashed line is how “uncorrelated data” from pulsars looks. The blue curve is the expected relation between pulsars when gravitational-waves pass by, known as a “Hellings-Downs curve.” (right) The same curve, with NANOgrav’s data overlaid. [Image: NANOgrav]

How long does it take for all these changes to happen and be noticed? The time it takes the gravitational wave to pass, which for the super-massive black holes can be many, many years. Which is why it has taken so long for astronomers to diligently time and retime all the pulsars in the array, and extract the ephemeral signal of the gravitational-wave background from the data.

[3] It’s really about people.

Science is often a long game, particularly science that probes the limits of human knowledge, and science done with advanced technology and tools that can’t fit in your pocket or on a laboratory bench. It takes hundreds and thousands of minds to conceive of what is possible, and then unflagging tenacity to solve each of the problems that arises until — in the end — a remarkable discovery is made. That long and arduous process means that people come and go, as they follow their own winding pathways to careers and life. But it also means we lose some people along the way who pass on, returning to the stardust from which we came. Here, I’d like to draw attention to just two of those people.

The first person was Ron Hellings. Ron is the Hellings of the “Hellings-Downs” curve, the swooping pattern of correlated signals from the scattered beacons in the pulsar timing array. He and his collaborator, George Downs, first wrote down what that pattern would look like and what pulsar astronomers should look for in a paper in 1983; it was only this week in 2023, forty years later, that their idea came to fruition.

Me and Ron Hellings in 2012, working on the details of a gravitational-wave observatory. [Image: S. Larson]

Sadly Ron passed away on 1 January 2022. At his memorial, when we talked about the important things Ron had discovered about the Universe, the Hellings-Downs curve was one of them.

I have the good fortune of being one of Ron’s academic descendants. I first met him when I was working on my PhD thesis, where we were thinking about the LISA gravitational-wave observatory. It was the beginning of a collaborative enterprise and a friendship that spanned a quarter of a century. We worked on many things together, including LISA, how to think about gravitational-wave signals, how to teach students, and a zillion other things in physics and astronomy. After I finished my PhD I spent two years as his postdoc, when he was at the Jet Propulsion Laboratory. It was an exhilarating and exciting time, and firmly set me on the path of my career today.

The second person was Steve Detweiler. By the time I was in graduate school, in the late 1990s, Steve was already famous in our community. Like most of those famous people, he was larger than life to us students, but he was always friendly. At meetings, he talked with us at coffee breaks, came to our talks, and sometimes went to dinner with us. I knew Steve for many years after we first met, and we would talk at conferences and meetings where our work on gravitational-waves overlapped.

Steve Detweiler. [Image: Eric Poisson]

Steve was well known for many things in his career, but in the late 1970s he was the first person to propose that pulsar timing could be used to search for gravitational-wave backgrounds; in no uncertain terms, his original analysis sent us down pathway to the discovery that was announced this week. 

Steve sadly passed away on 8 February 2016, just three days before the first announcement of the discovery of gravitational waves, and seven years before this week’s announcement of the confirmation of his idea for how to sense the Cosmos anew.

For me, Steve was more than a scientific acquaintance. There came a time when I had to prepare my dossier for tenure as a University professor. The process involves a robust independent evaluation of a person’s contribution to the scientific enterprise. For part of it, the University asks several experts from around the world to make a blunt assessment about the tenure dossier. I got to pick two people, and the University picked four; needless to say it is a terrifying prospect, especially for those of us who don’t have the global stature many of our colleagues have in the field. But I asked Steve to write one of my assessments, and he agreed. I have no idea what he said (his letter was confidential), but whatever it was, the University tenured me, and I owe Steve a great thanks. 

My stories and relationships with these senior scientists in the field are not unique — all of us have been encouraged, mentored, and brought into the great adventure of science by colleagues like Ron and Steve. At the NANOgrav press conference, our colleague Maura McLaughlin pointed out that the NANOgrav collaboration involved hundreds of graduate students, undergraduates, and even high school students. Every one of these contributed their time, their unique enthusiasm and energy, and their skills to making the discovery happen. 

Not everyone, but some of the members of the NANOgrav collaboration at a recent meeting. People make science happen. [Image: NANOgrav]

The scientific work kept them in the game, growing their skills and propelling them on to whatever is next in their personal journeys. Some of them will go on and become pulsar-timing gravitational-wave astronomers, to be sure. Some will not, but will still become astronomers or physics professors and mentor students of their own. But not all of them — a good many of them will become teachers, or doctors, or engineers, or business leaders, or accountants, or any of a thousand other careers that make the world go round. And in them all, some of what they learned as part of the pulsar-timing-array community will go along with them.

In the end, it’s all about people, and that is the true legacy — the true magic — of the wondrous discovery of the nanohertz gravitational-wave background.

My heartfelt congratulations, respect, and admiration goes out to all my friends and colleagues who made this discovery possible. Excelsior!

The Hardest Thing About Science II: Nouns & Verbs

by Shane L. Larson

Friends and family who travel around with me know I have a fatal weakness for one of the most ephemeral manifestations of the human brain: museums. Museums ostensibly exist for the singular purpose of capturing and showing what we as a species have learned, what we have discovered, and what still gives us wonder about the vast and mysterious world around us.

A “Little Free Library,” one of the modern forms of libraries, found in neighborhoods around the world.

In many ways, they are like their sister institutions, an equally ephemeral result of our unique brains: libraries. Libraries ostensibly exist for the singular purpose of storing the knowledge our species has accumulated, dispersed freely and at will to anyone who walks through the doors. I have a fatal weakness for libraries as well.

What do I mean by fatal weakness? I mean if I walk into one of these spaces, I’m consumed by it. In a museum, I linger and dwell at every exhibit, I read the detailed descriptions, I go back to previous exhibits to see how it is all connected. In a library, I walk down the aisles brushing my fingers lightly over the spines of books, drinking in the titles, sometimes pulling one off the shelf to thumb through the pages.

Every now and then, I ponder why we first decided to create these museums and libraries. Often when people think about museums and attempt to describe them, they describe the things there: artifacts, rocks, shards of lost civilizations, exquisite pieces of art, stuffed creatures that once roamed the wilds. 

Consider what you might see if you visit the Adler Planetarium in Chicago. There you can see a star show on the planetarium dome, touch a fragment of the dwarf planet Ceres with your own bare hand, see a life-size model of the Opportunity rover on Mars, and stand next to the Gemini 12 capsule that carried Jim Lovell and Buzz Aldrin around the Earth for almost four days in 1966. 

The Gemini 12 capsule, on display at the Adler Planetarium in Chicago.

But these are all things, and while the things are a focal point that draws you into the museum, they are not why you are there. You stare, and linger, and imagine something quite different and ephemeral. What is that? 

Dr. Michelle Larson, the President of the Adler, describes this dichotomy  as “nouns” and “verbs.” The nouns are what attract our attention, but what we are looking for and hoping to find are verbs. 

Standing in front of Gemini 12, a thin pane of plexiglass keeping you barely a half meter away, you reach out your hand. What are you doing? Hoping to verify the construction of aluminum? Check that the paint is peeling? No, much more. 

Closeups of the Gemini 12 capsule, showing the cramped space of the crew cabin (left), and the scorched heatshield (right).

The almost involuntary movement of your hand is because your brain is imagining what it was like to hurtle through the vacuum of space at nearly 28,000 kilometers per hour (more than 17,000 miles per hour), protected by the thinnest veneer of metal and insulation — was it terrifying or exhilarating or both? You look at the tiny window, and try to imagine seeing the color and light that was seen as the capsule plummeted down to Earth on the way home. The blast pattern of char on the back of Gemini 12, where the heat shield protected Lovell and Aldrin from the 2700 degree Celsius inferno, makes you wonder: if someone touched the window would it feel warm? Staring at the tiny confined space where the astronauts lived for almost four days you wonder: did it smell in there?

The Gemini 12 capsule, the noun, is just a vehicle to stimulate your thinking about the experiences, the verbs. 

This spills over into hobbies. Consider birdwatching. For some of us, birds are sortable at best into “robins,” “ducks,” and “little brown birds.” But for people who identify as birders, there is a certain unconstrained joy that people find in seeing the widest possible variety of our feathered friends as they can. They meticulously stare at birds through binoculars in the backyard, slog down park trails to remote copses of trees, and diligently put food and water in the backyard, all to be afforded a chance to see a blue-winged teal, or an eastern meadowlark, or a tufted tit-mouse.

A collection of birds from the winter in Illinois. A bluejay (top left), a tufted titmouse (lower left), and a cardinal (right). [Photos: M. Larson]

The birds are nouns, but birders aren’t collecting birds. They are collecting the experience of seeing birds, the verbs of birding. Birding is a verb! The joy is seeing the delicate splash of color of feathers iridescent in the sun, of projecting your own joy on a bluejay who looks thrilled to have a peanut in its mouth, or hearing a mother cardinal squawking at her fledglings encouraging them to take wing for the first time.

Looking at the Moon through a telescope or binoculars always fires the imagination. [Photo: S. Larson]

Amateur astronomers are the same way. We stand out in the backyard, hunkered down in our winter jackets against the cold, peering intently into the eyepiece of a telescope, straining to see photons that have spent two million years sailing the void from the Andromeda galaxy to Earth. The telescopes, the photons themselves, are just nouns. They are cool things unto themselves. But the astronomer is experiencing the light, drowning themselves in the existential awe of imagining the enormous gulf that photon has crossed to ultimately fall into their eye. Perhaps the light originated right next door, on the Moon, or perhaps it started its journey long, long ago far across the Cosmos in a star in a galaxy so far away humans haven’t named it. That light journeyed for longer than humans have been on Earth, and ended its voyage rattling through a few telescope mirrors and terminating on the retina of an eyeball. Imagine the journey that light took. 

All of the practice of science can be thought of in this way: it’s nouns and verbs. The nouns are the things you get taught, that you can look up on Wikipedia, that you hear about on the news. Science is the process of acquiring knowledge. Knowledge is a noun. Science is a verb.

Consider a journey in your mind into the deepest levels of your body, to the nuclear heart of your cells where the secrets of life are hidden away. Today we know that in the nucleus of every one of your cells, we can find DNA — a long ladder of matched molecules (denoted A, C, G, and T). The order of those molecules along the billion-rung DNA ladder spell out the unique information needed to create and define every single living thing on Earth. But there was a time when we didn’t know that at all. The first people to know about the the delicate double helix of this master molecule were Rosalind Franklin and her graduate student Raymond Gosling, who in 1952 took the very first picture of the molecule by bombarding it with x-rays. Today that picture is known as “Photo 51,” and its role in the discovery of DNA’s structure is storied and fraught with all too human conflicts.

Photo 51, originally captured by Raymond Gosling and Rosalind Franklin in 1952. [Image: Wikimedia Commons]

Stare at that photo for a moment, the way scientists in the 1950’s did. Look carefully at the twist and weave, and see the rungs connecting the sides of the ladder. DNA is incomprehensibly smaller than your eye can see, but the picture captures its delicate form and spells out the previously unknown truth of how you and I and every lifeform on Earth are one with each other, siblings on the deepest levels.

Now lift your head up, and soar out to the enormously larger scale of the solar system. Voyager is NASA’s longest lived space mission, currently 45 years old and still pinging Earth with its lonely beacon as it sails beyond the Sun, farther from home than any object ever made by humans. But in early 1979 when it flew past Jupiter, it was young and in the prime of its life. It carried a suite of instruments to sense and record everything it could as it passed by the largest planet in the Sun’s family. Among the most precious things Voyager did was take pictures, and send them home to Earth like any good interstellar tourist might. Before Voyager even arrived at Jupiter, we knew about the “Great Red Spot.” It is a massive hurricane-like malestrom, twice the size of the planet Earth. It has been known to exists for the entire 400-years that humans have had telescopes and first pointed them at Jupiter; we have no idea how old it really is. 

Voyager I view of the Great Red Spot as it approached Jupiter in 1979. [Image: NASA/JPL]

But just look at the Great Red Spot, the way Voyager did. Observe it, study it. It is exquisite in form, in shape, in complexity, in color. It almost doesn’t look real. If you saw that picture hanging on my wall, you might think it was a painting, a creative outburst of some exquisite artist here on Earth. But it is indeed a painting, a massive and beautiful canvas of chaotic color made by Nature itself.

It is easy to get swept up in the nouns of science: knowing the exact genetic code for slime molds, the chemical structures of ant pheromones, the age of the oldest crocodile fossils, the distance to the farthest quasar, the diameter of the Great Red Spot, the number of teeth a great white shark has, or the temperature at the heart of the Kilauea Volcano. These are great things science has taught us. But they are not science in and of themselves. 

Science is the art of inventing ways to do the hard work of discovering. It may sound simple to figure out how many teeth a great white shark has, but it probably isn’t. It seems obvious perhaps that it is “hot” in the center of Kilauea, but I assure you no human has or could survive there. The how of getting all these bits of information, the experience of discovering, and expansion of our thinking about the world around us — that is science.

This is one of the hardest things about practicing science in the modern world: hanging on to the verbs, remembering the verbs, and giving them voice.

Science is a verb.

——————————————————-

This post is the second in a short series pondering what kinds of things make science difficult. The posts so far in this series are:

1: The Hardest Thing About Science – Language

2: The Hardest Thing About Science – Nouns & Verbs (this post)

The Hardest Thing About Science I: Language

by Shane L. Larson

One of the “features” of the modern world is memes percolating through our social media feeds, online browsing, and texts from friends. Sometimes these memes are humorous images, sometimes they are captures of tweets and posts, sometimes they are interesting facts. Let’s spend a few moments considering these last ones.

Examples of common memes that relay information or observations about science [Images via your favorite local internet browser].

Memes that relay “interesting facts” are often tidbits of history, trivia, or scientific knowledge that are surprising or provocative. Many of these memes are absolutely correct, yet surprising, and they get rebroadcast over and over again.

Why are such memes surprising and appealing? Sometimes they remind us of how little we know, or how it used to be when we were in school, or how silly complex questions can sound. They play with our deeply rooted notions of humor, playing word or pun games that juxtapose everyday language against the language of science. Chemistry memes are particularly good at this, where designations for the chemical elements — the 92 naturally occurring substances that the Universe creates everything from — are used to create words or funny turns of phrase. Like this meme about the element mercury, represented by its chemical symbol “Hg” (which comes from the Latin word for mercury, hydrargyrum — literally “liquid silver”).

Sometimes the reason is the propositions of science are used as beacons of stability in a world rife with randomness and illogic. Particularly in today’s world, where ideological arguments boiled down to soundbites are casually tossed around without much thought, people long for the ideals of impassioned debate moderated by reason and data. This is of course the standard that science aspires to, so memes promoting such ideals are popular.

But the memes of considerable interest are the ones that give you pause, and provide a delectable moment of cognitive dissonance. They challenge your thinking and world-view about something that seems ordinary, but apparently is not. 

Consider this very common repeated science factoid about the color magenta.

If you are like most people, you may read this and go, “What? WTF does this mean? Of course magenta exists! Look at this shade of lipstick right here!”

But to understand what is going on here, we have to dissect every little bit of the meme. First, of course “magenta” exists, because that square of color is clearly there, and recognizable in the array of colors people might call “magenta.” But the second part is the piece to consider carefully: it is a color your brain is using to interpolate between red and violet. This is where the science part of this factoid is. It has been presented to drive you into cognitive dissonance, but no effort has been made to really help you understand what it means in the concrete world of science… this is the failure of such memes.

It does, however, illustrate one of the hardest things about science: the imprecision of language. Human language, which we depend on every single day and use as a malleable all-purpose tool, cannot easily convey with precision and accuracy what science has to say about most phenomena in the world. Color is a classic example. What does a scientist mean if they make a pithy statement like “magenta does not exist”? They mean something very precise, but the language of our common vernacular means something quite different.

Consider the color in this image. What color do you name this? Show it around to family and friends and ask them what color they call it. You will get a wide range of answers: green, yellow-green, fluorescent green, fluorescent yellow, fire-engine green, safety-vest yellow. Well, what color is it? We all recognize this color, but there is no universal name for it, though using any of these names mentioned, and a few examples, would quickly firm up the color under discussion in conversation.

But that isn’t precise enough or good enough for science. Scientists need to know exactly what color is under discussion — perhaps they are trying to create an LED light to create that color, or making a sensor that responds only to that particular color when it is scanned. In this case, this color is very close to the dominant color of light shed by our parent star, the Sun — the reason we use this color for attention and safety is your eye has evolved over millions of years to be sensitive to this color.

The “blackbody spectrum” of the Sun. The hill-shaped curve shows how much light the Sun emits in each color, and it peaks in the “safety-vest yellow” range of colors (at a wavelength of 500 nanometers). [Image: S. Larson]

So what do scientists do, when language isn’t up to the task? We layer on a bit of mathematics. In the case of color, physicists use a number called wavelength (often denoted by a lower case Greek letter lambda: λ). In the classic rainbow spectrum of light, cast by raindrops or sun-catcher prisms, or bevels on your windows, every single color has a unique number that scientists use to identify it.

The approximate colors and associated wavelengths of light that are visible to the human eye (the “visible spectrum”). [Image: S. Larson]

In the communication of scientific ideas, this ability to clearly and unambiguously quantify something is critical. Consider the following two conversations about color:

Conversation 1:

    Father: I put your red jacket in the closet.
    Daughter: I don’t have a red jacket.
    Father: Yes you do, you wear it every day.
    Daughter: Pop! That is burgundy.
    Father: <blank stare>

Conversation 2:

    Astronomer 1: It was too red to show in the image.
    Astronomer 2: The camera should have picked it up. 
    Astronomer 1: The wavelength was around 720 nanometers.
    Astronomer 2: Oh, you mean really red.

As astronomers, we still depend on language just like everyone else, but we have a mechanism to fall back on more precise statements and specifications needed to understand the world around us. In the case of color, that is wavelength.

But what about the magenta? What does it mean that it “doesn’t exist”? It means that for a scientist, there is no quantifiable number — no wavelength — that identifies where in the spectrum of light the color you and I call “magenta” can be found. It cannot be found in the spectrum! Yet it clearly exists when you and I stare at this little colored square. It is, in fact, a mixture of pure colors from the spectrum — the violet and the red mentioned in the original meme.

In the rainbow spectrum, where each color has its own unique numeric label, if you take a bit the violet color, and mix it with a bit of the red color, and throw that light at your eye, your brain says “whoa! look at that magenta!” 

In many ways, the meme is being dishonest to get a shock out of you. The amount of violet and red to be mixed can be quantified to make different shades of magenta — otherwise printers and lipstick makers would have a much rougher time making things this color! There is an exact, quantifiable way to specify every shade of magenta you put on the table. 

Nature can make magenta, but Nature doesn’t make magenta as a fundamental building block.

Salt crystals are not fundamental objects; salt itself is a combination of fundamental elements, sodium and chlorine. [Image: Wikimedia Commons]

It’s no different than elemental chemistry. “Salt” does not exist on the periodic table, but salt clearly exists in the same way magenta exists. In the fundamental, quantifiable world of the chemical elements (the building blocks of which everything on Earth is made), there are two uniquely identified substances: one is called sodium (Na) and one is called chlorine (Cl), and when I bond them together, I get something that is not elemental, but a mixture that we call NaCl — sodium chloride, or “salt.”

Saying something “doesn’t exist” has a multitude of interpretational meanings, but it means something very specific and very precise.  In the context we’ve been discussing here it doesn’t mean you can’t find something you and I would call “magenta” in the Cosmos — it means none of the fundamental building blocks of color, the rainbow of light, are called “magenta.”

This is one of the hardest things about science. Language is evocative and emotional and nuanced and, ultimately, imprecise. And since we are social creatures who in large part think in terms of language and act in response to language, it makes it hard — very hard! — for our brains to engage in the discovery of the world around us with the rational, quantifiable approach of science.

Moreover, it is hard to express personal enthusiasm and joy for the wisdom and knowledge that science has brought our species, when science itself is ideally more grounded — that dichotomy make the communication of science using this ratty tool we call “language” all the more difficult.

But we still try. With a few funny graphics and memes, a few stories and quips, and a few written words like these ones here…

——————————————————-

This post is the first in a short series pondering what kinds of things make science difficult. The posts in this series are:

1: The Hardest Thing About Science – Language (this post)

2: The Hardest Thing About Science – Nouns & Verbs

Everything’s Gonna Be Alright

by Shane L. Larson

The inimitable Mary Fahl has a remarkable song that I listen to all the time, especially on days when it seems impossible that the world has not totally fallen apart. It is a sonorous and passionate piece called “Everything’s Gonna Be Alright.” It opens:

Blind Willie Johnson in a capsule singing ‘bout the soul of man
Encoded traces of the human race and what we understand
A human choir out in the distance trav’ling by a satellite
Symphonic strains of our existence burned into a single byte

Mary Fahl performing “Everything’s Gonna Be Alright.”

For the uninitiated, Mary’s song may seem strange or obtuse — lyrical renderings of language that may have philosophical meaning if contemplated long enough, or may inspire deep visceral emotions if interpreted in certain ways, or simply seem to be pleasant nonsense in the way only songs and poetry can be.

But in reality, Mary’s song is a tribute, heartfelt and full of wonder, for one of our species’ most audacious and hopeful acts: the creation of a message that will far outlive our civilization, promising whoever hears it that we are sometimes better than we often are. The message was created, physically engraved in precious metals, and cast out into the wild voids of the Cosmos, never to be seen again.

That message is known as the Voyager Golden Record. Two copies of the record were minted from disks of copper plated in gold, shrouded beneath protective covers of aluminum, and mounted on the side of each of the two Voyager spacecraft. 

The Voyager Golden Record; the panel on the left shows the cover (inscribed with information to decode the record), and the panel on the right shows the record itself. [Images: NASA/JPL]

Launched 16 days apart in the autumn of 1977, the Voyager spacecraft were ostensibly part of humanity’s first reconnaissance of the solar system, sent to explore the giant worlds of the outer solar system — Jupiter, Saturn, Uranus, and Neptune. They swung by each world, dutifully snapping pictures and radioing their precious scientific data back to the distant rock from which they hailed. As they passed by each world, gravity latched on to them, propelling them ever faster and farther, on to their next destination.

Voyager flight paths through the solar system [Image: NASA/JPL]

Voyager 1 passed Saturn in November of 1980, and the Ringed Planet flung it up and out of the plane of the solar system, toward the constellation of Ophiuchus. In August of 1989, after a twelve year journey, Voyager 2 passed by Neptune, letting the icy giant’s gravity swing it down and out of the solar system, propelling it in the direction of the constellation Sagittarius. After fleeting and tantalizing glimpses of our cosmic neighborhood, the Voyagers have started the long, slow sail to the stars. Today they are the most distant physical artifacts of the human race, both of them more than 20 billion kilometers away, the Sun and Earth mere flecks of distant light.

Powered by small nuclear generators, the Voyagers’ energy is nearly spent. They will dutifully continue to transmit faint bleeps of information back to Earth, but within a decade or so they will fall silent and grow cold, hurtling ever onward toward the stars. Time, space dust, and cosmic radiation will take their toll on these artifacts of Earth, but the Golden Records were designed to stall such inevitable decay for as long as possible. Made of metals that are unreactive and change slowly over time, and encased behind protective aluminum covers, they should resist the long slow death, surviving for a billion years or more..

But what possibly could we have put on the Golden Records to warrant such care and concern about their survival? Mary Fahl told us up front:

Encoded traces of the human race and what we understand

Within the limitations of a physical object that could survive a billion year journey into deep space, we captured what we could about our species, the planet on which we live, the lifeforms we share the Earth with, and the meager understanding of the Cosmos we have gained. Together with greetings in many languages of the planet, and a selection of music from around the world, we engraved the information on 12-inch disks of gold covered copper, and sent them to the stars. It was a gesture of hope and optimism that, in some imagined future, an intelligent species somewhere across the empty sea of space might stumble across Voyager and be able to know something about who we were, faint echoes of a lonely planet and species that once dreamed of sailing to the stars.

Blind Willie Johnson [Image: Wikimedia Commons]

The key elements of the Voyager record are the protective cover, an included stylus (phonograph needle) to play the record, 115 images, a collection of the “sounds of Earth,” spoken greetings in 55 languages, and 90 minutes of music in 27 tracks. Blind Willie Johnson is the second to last track, singing  Dark Was The Night, Cold Was The Ground, a blues Gospel song, with no words but Johnson murmuring and humming along with his soulful guitar picking.

By today’s standards, the amount of data on the record is miniscule — a handful of images that are 512 x 384 resolution, and only 90 minutes of music. But that’s all there is, a small snapshot of life on Earth at the end of the 20th Century. It is likely one of the only artifacts of humanity that will survive our species; for some distant intelligence that might someday find Voyager, it is the only thing they will ever know of us.

The assumption we are making is that whomever might find Voyager will make an attempt to decode the Record. It’s an all together human assumption — if you found a bottle washed up on the seashore, a message carefully preserved inside, would you open the bottle to read it? Of course you would! In our optimism, we trust the receivers of our message will do the same.

On the surface, it seems to be an audacious thought, that a message encoded on a facsimile of a phonograph record could be received and decoded by an extraterrestrial who knows absolutely nothing about us, our technology, our species, our cultures, or our languages. But the message was designed with precisely that concern in mind. Astronomers call the idea of receiving such a message “communication without preamble,” and believe understanding it is predicated on a single fact: that the receiving civilization is technologically skilled.

The Voyager record cover provides protection, but also has information about how numbers are expressed (the “barbell” in the lower right is a hydrogen atom, whose properties should be known), instructions for how to play the record (the image of the stylus on the circle in the upper left), instructions for how to get data off the record (the information on the upper right, showing the data and the first image), and a map of where Voyager came from (the starburst on the lower left). [Image: NASA/JPL]

One of the great truths of the Universe, and perhaps the greatest mystery, is that everything is governed by an immutable set of rules that we call The Laws of Nature. The idea, the logical chain of reasoning, is that if you are capable of travelling into space to discover Voyager, it means you have a deep understanding of those self-same laws, enough so that you can harness them to travel the void of space yourselves. So we encoded the Voyager message using the common foundations of astronomy, physics, and mathematics that apply in every corner of the Cosmos, and trust that an understanding of those foundations will provide enough of a clue to decode Voyager’s precious cargo of sounds, music, and images. 

If you think deeply about this, you might argue that an alien species that recovers Voyager may not have eyes to see as we do, so images may not carry the same meaning. They may not have ears to hear as we do, so music may not be perceivable in the same way. But consider: there are many phenomena in Nature that our senses cannot perceive, yet our intellect and technology make us perfectly capable of detecting and understanding. If an extraterrestrial species is technologically capable, we think they will similarly be able to apply their intellect to understand the story Voyager has to tell.

How do you decide what to include in a message you are sending to the stars? What do you put in a time-capsule to represent our planet and ourselves to an audience we will never know? What do you send to a world and a biology and a history and an intellect completely alien to our own? What do you want beings a million years from now to know about us?

We could be cynical, we could be optimistic, we could be realistic, we could be practical. What should we be?

It is often pointed out that we could have included images and messages about our great failings. The wars we fight, the violence we inflict on one another, our great failings in justice and equity for all the citizens and life of the planet. We could have included images of atomic mushroom clouds, of dead school-children, of wasted and decimated landscapes destroyed by our short-sighted obsessions. But we didn’t do that. We took a very neutral stance, perhaps a sanitized vision of our world. We included pictures of our planet from space, of a tropical island, of a mother and child, of a farmer in Guatelmala, and 111 others. A cynical person might suggest we were being overly deceptive, and not showing the truly ruthless and sad character of our species. Perhaps, but I think not.

Just a few of the images included on the Voyager Golden Record. See a more complete list at NASA’s Golden Record Site. [Images: NASA/JPL]

No, flipping through the image library of the Voyager Golden Record one also gets the sense that this is not just who we are, but what we hope we are — a species that is living through the challenges of our own adolescence, a species that is for the moment surviving, and a species that aspires and believes that many thousands of years hence, our descendants will still be here, wiser and better off than we. We tried to choose a series of images that say we learned enough to build Voyager, and while we’re aware of the dangers we currently face, we are also aware that we are part of a much larger Cosmos.  Our meager collection of images and music is a realization of what we have learned, manifested in the optimistic act of constructing an impossibly limited message containing a few precious tidbits of life on Earth, from a species called “humans.”

And we tossed the message into the Cosmic Void, knowing not where the tides of space might take it.

There is absolutely no consequence if Voyager is never found, nor if the message is never decoded. There is a certain solace we gain from the mere notion that it might be found and might be decoded. Perhaps that solace is rooted in a deep fear — the fear that we are alone in the Cosmos, and everything that we are and think and do will someday perish, extinguished utterly from the Universe.

But I much rather like to think that the solace is rooted in optimism. We believe that it is worth shouting into the Void, shouting that we were here and this is who we were. We believe that, perhaps, there will be beings as intelligent and curious and emotional as we, and that they too might find joy in the discovery of Voyager. We imagine they might feel inexorably compelled to decode the carefully constructed message, and discover that they also are not alone in all the expanse of the Cosmos. We imagine that they too might be struggling through their own adolescence, hoping to not destroy themselves. We imagine that if they receive this small, meager message from Earth, the knowledge that they are not alone might help them somehow. We imagine that such a message might help us.

It is remarkable to think that the act of creating the Voyager Record is an act of optimism, and precisely what Mary Fahl’s lyrical exploration suggests to me. It suggests that despite all the challenges our species faces, despite all the clear failures that we foist upon ourselves, that some part of us still knows the remarkable things we can achieve, and we imagine the good that could result.

In days of gloom, in days of sadness, no matter what we do here on Earth, Voyager sails ever onward, its Golden Record cradled carefully on board, a message for a billion years from now. Perhaps, as Mary noted, “everything’s gonna be alright.”